El trapecio es considerado una de las formas de cálculo más amenazantes para los estudiantes, por lo tanto hemos decidido brindarles un resumen de la idea general detrás del trapecio y explicarles las propiedades del mismo y presentarles algunos tipos de trapecios.
Ejercicios de Trapecio para Noveno Grado - Problemas y Soluciones
Practica cálculo de área, perímetro y propiedades de trapecios isósceles y rectángulos. Ejercicios resueltos paso a paso para estudiantes de noveno grado.
- Calcular el área de trapecios usando la fórmula con bases y altura
- Identificar y clasificar tipos de trapecios: isósceles, rectángulo y paralelogramo
- Resolver problemas de perímetro y encontrar medidas desconocidas en trapecios
- Aplicar propiedades de ángulos adyacentes en trapecios isósceles
- Determinar alturas y bases usando datos del área del trapecio
- Analizar relaciones entre triángulos y paralelogramos dentro de trapecios
Entendiendo la Trapecios
Características del trapecio
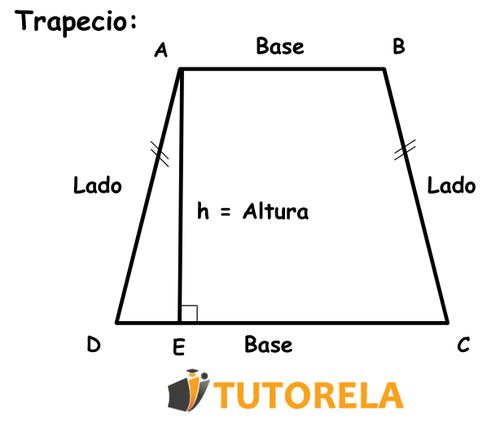
Un trapecio es un cuadrilátero basado en 4 lados como cualquier otro,
pero especial en que siempre tendrá dos lados paralelos llamados también bases, las cuales las podemos llamar base mayor y base menor
y también tendrá dos lados opuestos entre sí también llamados lados .
Practicar Trapecios
Dado el trapecio ABCD
Dado en cm: AB=4 DC=8
Área del trapecio en cm² S=30
Halla la altura del trapecio
ejemplos con soluciones para Trapecios
¿En todos los trapecios isósceles las Ángulos de la Base son iguales?
La respuesta es sí, ya que según la ley en todo trapecio isósceles los ángulos de la base son iguales entre sí.
Respuesta:
Verdadero
Dado el trapecio:
¿Cuál es el área?
Fórmula del área de un trapecio:
Reemplazamos los datos en la fórmula y resolvemos:
Respuesta:
52.5
Dado el trapecio ABCD
Dado en cm: AB=2.5 base DC=4 altura h=6
Calcula el área del trapecio
Primero recordemos la fórmula del área del trapecio:
Reemplazamos los datos en la fórmula:
(2.5+4)*6 =
6.5*6=
39/2 =
19.5
Respuesta:
Dado:
trapecio isósceles.
Halla a x.
Dado que el trapecio es isósceles y los ángulos en ambos lados son iguales, se puede argumentar que:
Sabemos que la suma de los ángulos de un cuadrilátero es 360 grados.
Por lo tanto podemos crear la fórmula:
Reemplazamos de acuerdo a los datos existentes:
Dividimos las dos secciones por 4:
Respuesta:
30°
Dado el trapecio de la figura, ¿cuál es su perímetro?
Para hallar el perímetro sumaremos todos los lados:
Respuesta:
24