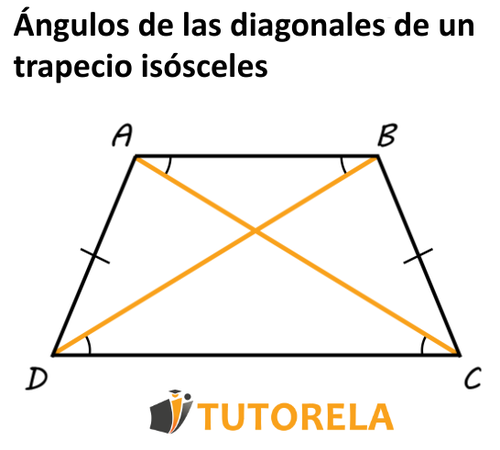
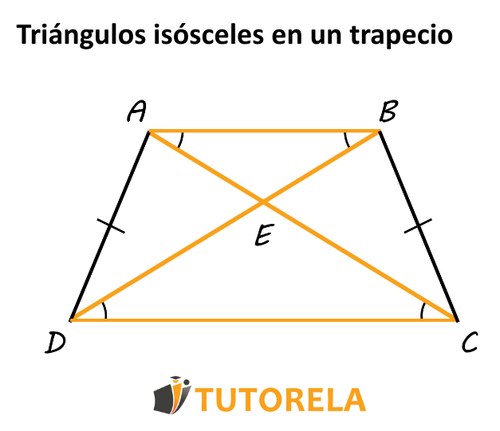
Las diagonales de un trapecio isósceles tienen la misma longitud.
Este teorema se cumple también a la inversa, o sea, podemos determinar que cierto trapecio es isósceles si sabemos que sus diagonales son iguales.
Puedes utilizar este teorema en el examen tal como lo ves y no deberás demostrarlo.
La segunda propiedad:
Dado el trapecio isósceles se cumple:
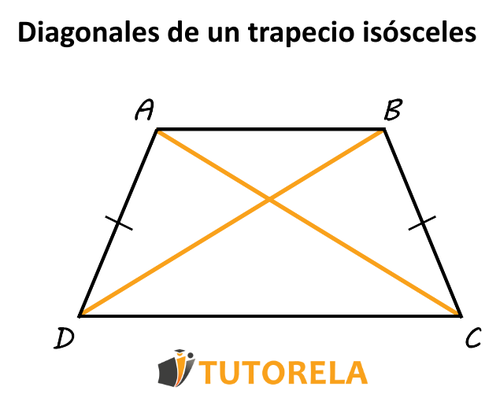
Observa- Deberás demostrar esta propiedad en el examen. La podemos demostrar basándonos en teorema de congruencia LLL.
Dado el trapecio isósceles se cumple:
Observa- Deberás demostrar esta propiedad en el examen. La podemos demostrar basándonos en teorema de congruencia .
Las diagonales de un trapecio isósceles crean, junto con las bases, ángulos iguales.
Los marcaremos.
Observa- Deberás demostrar esta propiedad en el examen.
Las diagonales de un trapecio isósceles crean, junto con las bases, dos triángulos isósceles.
Nos percataremos de que se trata de y de .
Marcaremos con color anaranjado los triángulos que se crean a partir de las diagonales y las bases:
Observa- Deberás demostrar esta propiedad en el examen.
Dado: \( ∢C=2x \)
\( ∢A=120° \)
trapecio isósceles.
Halla a x.
¿En todos los trapecios isósceles las Ángulos de la Base son iguales?
Dado que: el perímetro del trapecio es igual a 22 cm
AB= 7 cm
AC= 3 cm
BD= 3 cm
Halla el tamaño de CD.
¿Las diagonales del trapecio necesariamente se cruzan entre sí?
Dado: trapecio isósceles.
\( ∢B=3x \)
\( ∢D=x \)
Halla a \( ∢B \)
Dado:
trapecio isósceles.
Halla a x.
Dado que el trapecio es isósceles y los ángulos en ambos lados son iguales, se puede argumentar que:
Sabemos que la suma de los ángulos de un cuadrilátero es 360 grados.
Por lo tanto podemos crear la fórmula:
Reemplazamos de acuerdo a los datos existentes:
Dividimos las dos secciones por 4:
30°
¿En todos los trapecios isósceles las Ángulos de la Base son iguales?
La respuesta es sí, ya que según la ley en todo trapecio isósceles los ángulos de la base son iguales entre sí.
Verdadero
Dado que: el perímetro del trapecio es igual a 22 cm
AB= 7 cm
AC= 3 cm
BD= 3 cm
Halla el tamaño de CD.
Como nos dan el perímetro del trapecio y no la longitud de CD, podemos calcular:
9
¿Las diagonales del trapecio necesariamente se cruzan entre sí?
Las diagonales de un trapezoide isósceles son siempre iguales entre sí,
pero no necesariamente se cruzan entre sí.
(Recordatorio, "cruce" significa que se encuentran exactamente en el medio, lo que significa que están cortados en dos partes iguales, dos mitades)
Por ejemplo, se traza el siguiente trapecio ABCD, que es isósceles.
Usando un programa de computadora calculamos el centro de las diagonales,
Y observamos que los puntos centrales no son G, sino los puntos E y F.
Eso significa que las diagonales no se cruzan.
No verdadero
Dado: trapecio isósceles.
Halla a
Para responder a la pregunta, debemos conocer una regla importante de los trapecios isósceles:
La suma de los ángulos que delimitan cada uno de los lados trapezoidales (no las bases) es igual a 180
Por lo tanto:
∢B+∢D=180
3X+X=180
4X=180
X=45
Es importante recordar que esa aún no es la solución, porque nos pidieron el ángulo B,
Por lo tanto:
3*45 = 135
¡Y esta es la solución!
135°
Dado: trapecio isósceles.
\( ∢B=2y+20 \)
\( ∢D=60 \)
Halla a \( ∢B \)
Dado el trapecio ABCD isósceles.
Dado en cm: BC=7 altura del trapecio h=5 perímetro del trapecio P=34
Calcula el área del trapecio
\( ∢D=50° \)
El trapecio isósceles
Cuál es \( ∢B \)?
Dado: \( ∢A=120° \)
El trapecio isósceles
Halla a: \( ∢C \)
Dado el polígono en el dibujo
¿Qué tipo es?
Dado: trapecio isósceles.
Halla a
Para responder el ejercicio, primero se necesita conocer cierta información:
En un cuadrilátero la suma de los lados interiores es 180.
El trapecio isósceles tiene ángulos iguales.
De aquí se deduce que la suma de los ángulos adyacentes a un lado del trapecio es 180°.
Convertimos esta conclusión en un ejercicio:
2y+20+60=180
Sumamos los ángulos relevantes
2y+80=180
Movemos las secciones:
2y=180-80
2y=100
Dividido por 2
y=50
¡Y esta es la solución!
120°
Dado el trapecio ABCD isósceles.
Dado en cm: BC=7 altura del trapecio h=5 perímetro del trapecio P=34
Calcula el área del trapecio
Como ABCD es un trapecio, se puede argumentar que:
La fórmula para hallar el área será
Como nos dan el perímetro del trapecio, podemos encontrar
Ahora colocaremos el dato que recibimos en la fórmula para calcular el área del trapecio:
50
El trapecio isósceles
Cuál es ?
130°
Dado:
El trapecio isósceles
Halla a:
60°
Dado el polígono en el dibujo
¿Qué tipo es?
Trapecio
Dado: \( ∢A=y+20 \)
\( ∢D=50 \)
trapecio isósceles.
Halla a \( ∢A \)
¿Los triángulos marcados son isósceles?
\( (ΔABE,ΔCED)\text{ } \)
Dado que: el perímetro del trapecio es igual a 75 cm
AB= X cm
AC= 15 cm
BD= 15 cm
CD= X+5 cm
Halla el tamaño de AB.
Dado que: el perímetro del trapecio es igual a 35 cm
AB= 10 cm
CD= 15 cm
El trapecio isósceles
Halla la suma de los tamaños de los lados.
Dado el trapecio ABCD isósceles
AD=AE
Halla los ángulos del trapecio y el ángulo \( \alpha \)
Dado:
trapecio isósceles.
Halla a
130
¿Los triángulos marcados son isósceles?
Verdadero
Dado que: el perímetro del trapecio es igual a 75 cm
AB= X cm
AC= 15 cm
BD= 15 cm
CD= X+5 cm
Halla el tamaño de AB.
20
Dado que: el perímetro del trapecio es igual a 35 cm
AB= 10 cm
CD= 15 cm
El trapecio isósceles
Halla la suma de los tamaños de los lados.
10
Dado el trapecio ABCD isósceles
AD=AE
Halla los ángulos del trapecio y el ángulo
A,B=110.5 | C,D=69.5 |