El trapecio es considerado una de las formas de cálculo más amenazantes para los estudiantes, por lo tanto hemos decidido brindarles un resumen de la idea general detrás del trapecio y explicarles las propiedades del mismo y presentarles algunos tipos de trapecios.
Trapecios
Características del trapecio
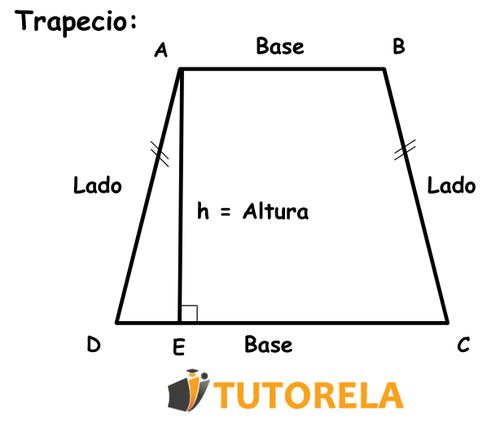
Un trapecio es un cuadrilátero basado en 4 lados como cualquier otro,
pero especial en que siempre tendrá dos lados paralelos llamados también bases, las cuales las podemos llamar base mayor y base menor
y también tendrá dos lados opuestos entre sí también llamados lados .
¡Pruébate en trapecio para noveno grado!
Calcula el perímetro del trapecio de abajo:
Tipos de trapecios
Existen varios tipos de trapecios que encontrarás durante tus estudios.
Por ejemplo, hay un trapecios donde las rectas miran en la misma dirección y se llama paralelogramo
Además, existe un trapecio que tiene dos lados de la misma longitud y se lo llama Trapecio isósceles. En el primer ejemplo, tenemos un trapecio de ángulo recto, el cual es un trapecio en el que la altura es igual al lado perpendicular a las bases de modo que se forman 2 ángulos rectos.

¿Quieres saber también cómo calcular el área de un trapecio y otras formas geométricas?
Si estás interesado en aprender a calcular áreas de otras formas geométricas puedes ingresar a uno de los siguientes artículos:
- ¿Cómo se calcula el área de un trapecio?
- Simetría en trapecios
- Diagonales de un trapecio isósceles
- ¿Cómo se calcula el perímetro de un trapecio?
- Cómo calcular el área de un triángulo
- El área del paralelogramo: ¿qué es y cómo se calcula?
- Área circular
- Área de superficie de prismas triangulares
- ¿Cómo se calcula el área de un rombo?
- ¿Cómo calcular el área de un hexágono regular?
- Área del rectángulo
- Cómo calcular el área de un ortoedro
En la página web de Tutorela encontrarás una variedad de artículos sobre matemáticas.
Calcula el perímetro del trapecio según los datos
Calcula el perímetro del trapecio de abajo:
Calcula el perímetro del trapecio de abajo:
Ejercicios con explicaciones sobre el tema Propiedades y tipos de trapecio
Ejercicio 1
¿Cómo calculamos el área de un trapecio?
Nos dan el siguiente trapecio isósceles con las siguientes características:
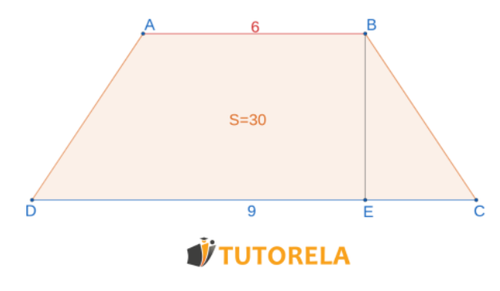
Tarea:
¿Cuál es su altura?
Solución:
Fórmula del área de un trapecio:
Sustituyendo estos valores en nuestra fórmula tenemos lo siguiente:
Y resolvemos:
Respuesta:
Altura es igual a .
Ejercicio 2
Dado el área de un trapecio que su base inferior es el doble de la base superior y veces mayor que la altura.
El área del trapecio es igual a (consigue ayuda a partir de )
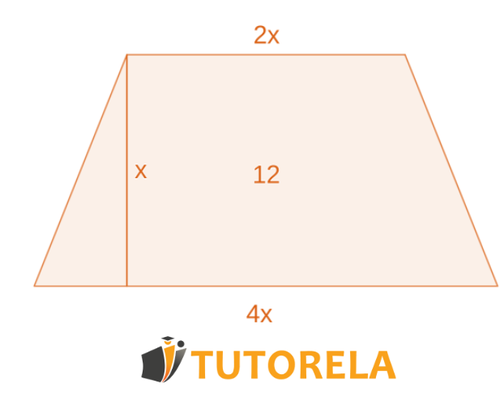
Tarea:
Calcula cuánto es el valor de .
Solución:
Dado que la base inferior es el doble que la base superior y veces más grande que la altura.
si dividimos todo entre
Ahora sacando raíz de ambos lados
Respuesta:
¿En el trapecio isósceles los dos pares de lados son paralelos?
¿En todos los trapecios isósceles las Ángulos de la Base son iguales?
\( ∢D=50° \)
El trapecio isósceles
Cuál es \( ∢B \)?
Ejercicio 3
Dado que es un trapecio isósceles con las siguientes características
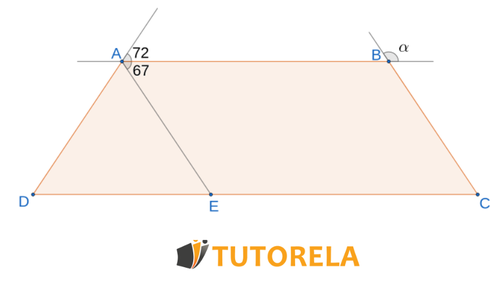
Tarea:
Encontrar los ángulos del trapecio y el ángulo
Solución:
La suma de ángulos adyacentes
Esto por que el es un triángulo isósceles
Frente a los lados iguales del triángulo
La suma de los ángulos adyacentes en el trapecio son iguales a
entre las dos bases
Ángulos opuestos por el vértice
Respuesta:
Ejercicio 4
Dado que es un trapecio isósceles
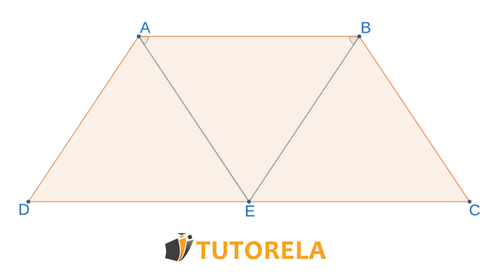
Tarea:
¿A qué es igual la sección del medio frente a en el triángulo que su base es ?
Solución:
--->
Dada la figura que:
La regla:
Los lados opuestos son iguales en , es igual a los lados
Lado =
Lado =
Ángulo =
Según el teorema de comprobación lado, lado, ángulo
Lados correspondientes entre triángulos superpuestos
Una sección de medio en un triángulo < es igual a la mitad del lado al que corresponde.
Sección media =
Respuesta:
Dado el siguiente trapecio:
Calcule el área del trapecio ABCD.
Dado el trapecio:
¿Cuál es el área?
Dado el siguiente trapecio:
Calcule el área del trapecio ABCD.
Ejercicio 5
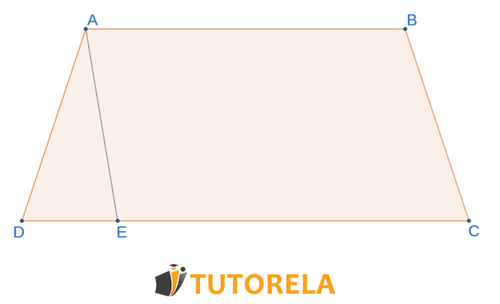
El área del trapecio
La recta crea el triángulo \( AED \) y el paralelogramo .
Se sabe que la razón del área del triángulo al área del paralelogramo es .
Tarea:
Calcula la razón entre los lados y .
Solución:
Para calcular la razón entre los lados usaremos la figura que:
Calculamos mediante la fórmula para encontrar la mitad del área y colocamos la razón.
Para resolver la ecuación, multiplique cruzando los factores.
Dividiendo todo entre tenemos lo siguiente:
La razón entre es
Respuesta:
Respuesta:

Preguntas de repaso
¿Qué son las características de los trapecios?
Las características del trapecio, serán aquellas que nos ayuden a definir o clasificar a qué tipo de trapecio nos estamos refiriendo, cabe recordar que existen diferentes tipos de trapecios, como lo son el trapecio isósceles, el trapecio rectángulo o un paralelogramo. Por ello es muy importante tomar en cuenta las características de cada uno de ellos.
¿Qué características tiene un trapecio rectángulo?
Las características del trapecio rectángulo son que tiene dos ángulos rectos, un ángulo agudo y uno obtuso, con eso generando que dos de sus lados sean iguales.
¿Cuáles son los elementos de un trapecio?
Como ya lo dijimos el trapecio es un cuadrilátero (4 lados) donde tiene dos lados paralelos, los cuales son llamados bases, regularmente consideradas como base mayor y base menor, cuenta con una altura y tiene 4 ángulos.
¿Qué es un trapecio isósceles?
Un trapecio isósceles es aquel que tiene dos lados iguales, los cuales serán los lados que unen a sus rectas paralelas, está es una de las principales características de este tipo de trapecios.
Dado el trapecio de la figura
Halla su perímetro:
Dado el trapecio de la figura, ¿cuál es su perímetro?
Dado el trapecio ABCD
Dado en cm: AB=2.5 base DC=4 altura h=6
Calcula el área del trapecio
ejemplos con soluciones para Trapecios
Ejercicio #1
¿En todos los trapecios isósceles las Ángulos de la Base son iguales?
Solución en video
Solución Paso a Paso
La respuesta es sí, ya que según la ley en todo trapecio isósceles los ángulos de la base son iguales entre sí.
Respuesta
Verdadero
Ejercicio #2
Dado el trapecio:
¿Cuál es el área?
Solución en video
Solución Paso a Paso
Fórmula del área de un trapecio:
Reemplazamos los datos en la fórmula y resolvemos:
Respuesta
52.5
Ejercicio #3
Dado el trapecio ABCD
Dado en cm: AB=2.5 base DC=4 altura h=6
Calcula el área del trapecio
Solución en video
Solución Paso a Paso
Primero recordemos la fórmula del área del trapecio:
Reemplazamos los datos en la fórmula:
(2.5+4)*6 =
6.5*6=
39/2 =
19.5
Respuesta
Ejercicio #4
Dado:
trapecio isósceles.
Halla a x.
Solución en video
Solución Paso a Paso
Dado que el trapecio es isósceles y los ángulos en ambos lados son iguales, se puede argumentar que:
Sabemos que la suma de los ángulos de un cuadrilátero es 360 grados.
Por lo tanto podemos crear la fórmula:
Reemplazamos de acuerdo a los datos existentes:
Dividimos las dos secciones por 4:
Respuesta
30°
Ejercicio #5
Dado el trapecio de la figura, ¿cuál es su perímetro?
Solución en video
Solución Paso a Paso
Para hallar el perímetro sumaremos todos los lados:
Respuesta
24
- Altura del triángulo
- Deltoide
- Área del deltoide:
- Suma de los ángulos internos de un triángulo
- Los lados o aristas de un triángulo
- Paralelogramo
- El área del paralelogramo: ¿qué es y cómo se calcula?
- Perímetro de un paralelogramo
- Maneras de identificar paralelogramos
- Simetría rotacional en paralelogramos
- Del cuadrilátero al paralelogramo
- Trapecios
- Simetría en trapecios
- Diagonales de un trapecio isósceles
- Área de un trapecio
- Perímetro de un trapecio
- Trapecio isósceles
- Rectángulo
- De un cuadrilátero a un rectángulo
- Del paralelogramo al rectángulo
- ¿Cómo se calcula el área de un rectángulo?
- El perímetro del rectángulo
- Rectángulos congruentes
- Ángulo exterior de un triángulo
- Cuadrado
- El área de un cuadrado
- De paralelogramo a cuadrado
- Segmento medio
- Segmento medio de un triángulo
- Segmento medio de un trapecio
- Área
- ¿Rombo, cometa o diamante?
- Diagonales de un rombo
- Simetría del rombo
- De paralelogramo a rombo
- El área de un rombo
- Perímetro
- Triángulo
- Tipos de triángulos
- Triángulo obtuso
- Triángulo equilátero
- Identificación de un triángulo isósceles
- Triángulo escaleno
- Triángulo agudo
- Triángulo isósceles
- Área de un triángulo
- Área de un triángulo rectángulo
- Área del triángulo isósceles
- Área del triángulo escaleno
- Área del triángulo equilátero
- Perímetro de un triángulo
- Áreas de Polígonos para 7º Grado
- Triángulo Rectángulo
- Área de un trapecio rectángulo
- Área de un trapecio isósceles
- Mediana en un triángulo
- Centro de un Triángulo - El Centroide - El Punto de Intersección de las Medianas
- ¿Cómo calculamos el área de figuras complejas?
- ¿Cómo calculamos el perímetro de los polígonos?
- Todos los términos en el cálculo de triángulos
- ¿Cómo calcular el área de un triángulo usando trigonometría?
- Orden de operaciones básicas: suma, resta, multiplicación y división
- Orden de las operaciones básicas (potencias)
- Orden de operaciones básicas: raíces
- El 0 y el 1 en el orden de las operaciones
- Inverso multiplicativo
- Orden de las operaciones: paréntesis
- La propiedad conmutativa
- La propiedad asociativa
- Cómo calcular el área de un ortoedro
- Potenciación de números enteros
- Las Tablas de Multiplicar
- Fracciones









