Considera un triángulo rectángulo, AB = 8 cm y AC = 6 cm.
Calcula la longitud del lado BC.
Uso del Teorema de Pitágoras: Aplicación de la fórmula
Considera un triángulo rectángulo, AB = 8 cm y AC = 6 cm.
Calcula la longitud del lado BC.
Dado el triángulo del dibujo. ¿Cuál es el largo AB?
Dado el triángulo del dibujo. Halla el largo AC
Dado el triángulo rectángulo:
¿Cuál es el largo del tercer lado?
Dado el triángulo ABC, halla el largo BC
ejemplos con soluciones para Uso del Teorema de Pitágoras: Aplicación de la fórmula
Ejercicio #1
Solución Paso a Paso
Para encontrar la longitud de la hipotenusa BC en un triángulo rectángulo donde AB y AC son los otros dos lados, usamos el teorema de Pitágoras: .
Aquí, y .
Sustituyendo los valores en el teorema de Pitágoras, obtenemos:
.
Calculando:
.
Tomando la raíz cuadrada de ambos lados:
.
Respuesta
10 cm
Ejercicio #2
Dado el triángulo del dibujo. ¿Cuál es el largo AB?
Solución en video
Solución Paso a Paso
Para hallar el lado AB, necesitaremos usar el teorema de Pitágoras.
El teorema de Pitágoras nos permite hallar el tercer lado de un triángulo rectángulo, si tenemos los otros dos lados.
Puedes leer todo sobre el teorema aquí.
Teorema de Pitágoras:
Es decir, un lado de un cuadrado más el segundo lado de un cuadrado es igual al tercer lado de un cuadrado.
Reemplazamos los datos existentes:
Extraemos la raíz:
Respuesta
cm
Ejercicio #3
Dado el triángulo del dibujo. Halla el largo AC
Solución en video
Solución Paso a Paso
Para resolver el ejercicio, tenemos que utilizar el teorema de Pitágoras:
A²+B²=C²
Reemplazamos los datos que tenemos:
3²+4²=C²
9+16=C²
25=C²
5=C
Respuesta
5 cm
Ejercicio #4
Dado el triángulo rectángulo:
¿Cuál es el largo del tercer lado?
Solución en video
Solución Paso a Paso
Usamos el teorema de Pitágoras
Reemplazamos los datos que conocemos:
Extraemos la raíz:
Respuesta
5
Ejercicio #5
Dado el triángulo ABC, halla el largo BC
Solución en video
Solución Paso a Paso
Para responder a esta consigna, debemos conocer el Teorema de Pitágoras
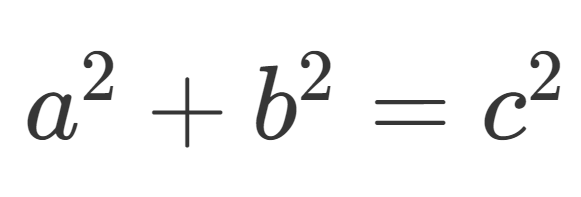
El teorema nos permite calcular los lados de un triángulo rectángulo.
Identificamos los lados:
ab = a = 5
bc = b = ?
ac = c = 13
Reemplazamos los datos en el ejercicio:
5²+?² = 13²
Intercambiamos las secciones
?²=13²-5²
?²=169-25
?²=144
?=12
Respuesta
12 cm
Dado el triángulo del dibujo. ¿Cuál es el largo BC?
Ejercicio #6
Dado el triángulo del dibujo. ¿Cuál es el largo BC?
Solución en video
Solución Paso a Paso
Para resolver el ejercicio es necesario conocer el Teorema de Pitágoras:
A²+B²=C²
Reemplazamos los datos conocidos:
2²+B²=7²
4+B²=49
Traspasamos las secciones:
B²=49-4
B²=45
Extraemos la raíz
B=√45
Básicamente esta es la solución, pero usando las reglas de las raíces, podemos descomponer la raíz un poco más.
Primero, descompongamos en números primos:
B=√(9*5)
Usamos la propiedad de raíces en la multiplicación: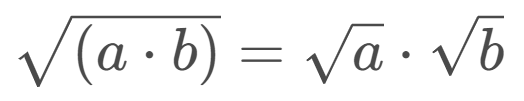
B=√9*√5
B=3√5
¡Esta es la solución!
Respuesta
cm