Familia de parábolas y=(x-p)2 - Ejemplos, Ejercicios y Soluciones

Familia de las parábolas $y=(x-p)^2$

En esta familia tenemos una función cuadrática un poco diferente que nos muestra, de forma muy clara, cómo la parábola se desplaza horizontalmente.
$P$ Indica la cantidad de pasos que la parábola se moverá horizontalmente, hacia la derecha o hacia la izquierda.
Si $P$ positiva: (hay un signo menos en la ecuación) - La parábola se moverá $P$ pasos hacia la derecha.
Si $P$ negativa: (y, por consiguiente habrá un signo de más en la ecuación ya que menos por menos equivale a más) - La parábola se moverá $P$ pasos hacia la izquierda.

Veamos un ejemplo:
La función $Y=(X+2)^2$

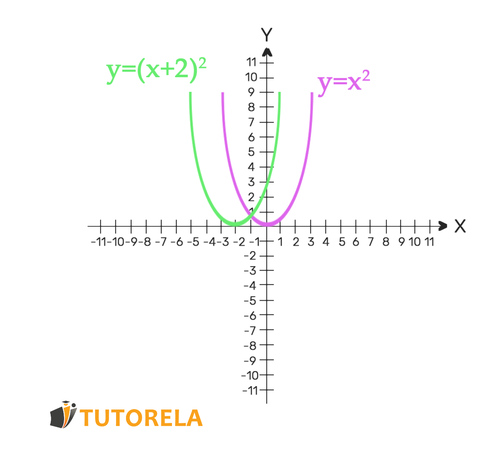
se desplaza hacia la izquierda dos pasos.
Veámoslo en una ilustración:

Explicación completa

Temas sugeridos para practicar con anticipación

Practicar Familia de parábolas y=(x-p)2

Ejercicio 1

Halle el dominio positivo de la función

$$ y=(x-2)^2 $$

Ejercicio 2

Halla la intersección de la función

$$ y=(x+4)^2 $$

Con el eje Y

Ejercicio 3

Halla la intersección de la función

$$ y=(x-2)^2 $$

Con el eje X

Ejercicio 4

Halla la intersección de la función

$$ y=(x-2)^2 $$

Con el eje Y

Ejercicio 5

Halla la intersección de la función

$$ y=(x-6)^2 $$

Con el eje Y

ejemplos con soluciones para familia de parábolas y=(x-p)2

Ejercicio #1

Halle el dominio positivo de la función

$y=(x-2)^2$

Solución en video

Solución Paso a Paso

En el primer paso colocamos 0 en el lugar Y.

0 = (x-2)²

Realizamos una raíz cuadrada:

0=x-2

x=2

Y así revelamos el punto

(2, 0)

Este es el punto extremo de la parábola.

Luego descomponemos la ecuación en forma estándar:

y=(x-2)²

y=x²-4x+2

Como el coeficiente de x² es positivo, aprendemos que la parábola es una parábola mínima (sonriente).

Si trazamos la parábola, parece que en realidad es positiva excepto por su punto extremo,

Por lo tanto el dominio de positividad es todo X, excepto X≠2

Respuesta

todo x, $x\ne2$

Ejercicio #2

Halla la intersección de la función

$y=(x+4)^2$

Con el eje Y

Solución en video

Respuesta

$(0,16)$

Ejercicio #3

Halla la intersección de la función

$y=(x-2)^2$

Con el eje X

Solución en video

Respuesta

$(2,0)$

Ejercicio #4

Halla la intersección de la función

$y=(x-2)^2$

Con el eje Y

Solución en video

Respuesta

$(0,4)$

Ejercicio #5

Halla la intersección de la función

$y=(x-6)^2$

Con el eje Y

Solución en video

Respuesta

$(0,36)$

Ejercicio 1

Halla el área positiva de la función

$$ y=(x+6)^2 $$

Ejercicio 2

Halla el área positiva de la función
$$ y=(x+5)^2 $$

Ejercicio 3

Halla el área negativa de la función

$$ y=(x+2)^2 $$

Ejercicio 4

Halla el área negativa de la función

$$ y+1=(x+3)^2 $$

Ejercicio 5

Para saber los puntos de intersección con el eje X

Reemplazamos $$ x=0 $$