La fórmula de las raíces - Ejemplos, Ejercicios y Soluciones

Tipos de Preguntas:
La fórmula de las raíces: Completar la ecuaciónLa fórmula de las raíces: Factorización de trinomios usando descomposiciónLa fórmula de las raíces: Fórmula faltanteLa fórmula de las raíces: Tercera potenciaLa fórmula de las raíces: Factorización del Máximo Común Divisor (MCD)La fórmula de las raíces: Uso de fraccionesLa fórmula de las raíces: Uso de fórmulas de multiplicación cortaLa fórmula de las raíces: Sistema de ecuaciones sin soluciónLa fórmula de las raíces: Identificando y definiendo elementosLa fórmula de las raíces: Completar la ecuación de una soluciónLa fórmula de las raíces: Ecuaciones con variables en ambos ladosLa fórmula de las raíces: Aplicando la fórmula con dos soluciones

¿Qué es la fórmula cuadrática?

La ecuación cuadrática, o de segundo grado, contiene 3 3 parámetros:

  • Parámetro a a representa la posición del vértice de la parábola en el eje Y Y . Una parábola puede tener un vértice máximo, o un vértice mínimo.
  • Parámetro b b representa la posición del vértice de la parábola en el eje X X .
  • parámetro c c representa el punto de intersección de la parábola con el eje Y Y .

Estos parámetros se expresan en la ecuación cuadrática de la siguiente manera:

aX2+bX+c=0 aX^2+bX+c=0

Es decir, estos son los coeficientes de las ecuaciones. Así es que para aplicar la fórmula cuadrática a la ecuación que presentamos anteriormente, solo necesitaremos ubicar los parámetros en la fórmula, de acuerdo a los coeficientes de la ecuación. 

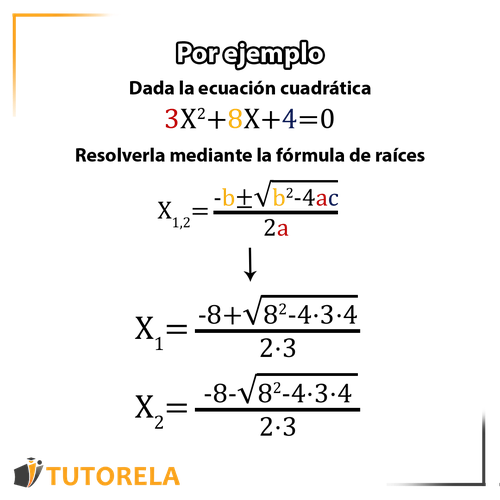
Por ejemplo:

3X2+8X+4=0 3X^2+8X+4=0

Por ejemplo a fórmula de las raíces para una ecuación de segundo grado 1

Explicación completa

Practicar La fórmula de las raíces

Ejercicio 1

Resuelva la siguiente ecuación

\( x^2+5x+4=0 \)

Ejercicio 2

\( x^2+9=0 \)

Resuelva la ecuación

Ejercicio 3

a = coeficiente de x²

b = coeficiente de x

c = coeficiente del número independiente


cuál es el valor de \( c \) en la función

\( y=-x^2+25x \)

Ejercicio 4

a = coeficiente de x²

b = coeficiente de x

c = coeficiente del número independiente


cuál es el valor de \( b \) en la ecuación

\( y=4x^2-16 \)

Ejercicio 5

a = coeficiente de x²

b = coeficiente de x

c = coeficiente del número independiente


cuál es el valor de \( c \) en la ecuación

\( y=5+3x^2 \)

ejemplos con soluciones para La fórmula de las raíces

Ejercicio #1

Resuelva la siguiente ecuación

x2+5x+4=0 x^2+5x+4=0

Solución en video

Solución Paso a Paso

Los parámetros se expresan en la ecuación cuadrática de la siguiente manera:

aX2+bX+c=0

 

Reemplazamos en la fórmula:

 

-5±√(5²-4*1*4) 
          2

 

-5±√(25-16)
         2

 

-5±√9
    2

 

-5±3
   2

 

El signo ± significa que tenemos que resolver esta parte dos veces, una vez con un más y una segunda vez con un menos,

Así es como más tarde obtenemos dos resultados.

 

-5-3 = -8
-8/2 = -4

 

-5+3 = -2
-2/2 = -1

 

Y así descubrimos que X = -1, -4

Respuesta

x1=−1 x_1=-1 x2=−4 x_2=-4

Ejercicio #2

x2+9=0 x^2+9=0

Resuelva la ecuación

Solución en video

Solución Paso a Paso

Los parámetros se expresan en la ecuación cuadrática de la siguiente manera:

aX2+bX+c=0

 

Identificamos que tenemos:
a=1
b=0
c=9

 

Recordamos la fórmula de las raíces:

נוסחת השורשים | הנוסחה

Reemplazamos de acuerdo a la fórmula:

-0 ± √(0²-4*1*9)

           2

 

Nos enfocaremos en la parte dentro de la raíz cuadrada (también llamada delta)

√(0-4*1*9)

√(0-36)

√-36

 

No es posible sacar la raíz cuadrada de un número negativo.

Y entonces la pregunta es de hecho irresoluble.

Respuesta

No hay solución

Ejercicio #3

a = coeficiente de x²

b = coeficiente de x

c = coeficiente del número independiente


cuál es el valor de c c en la función

y=−x2+25x y=-x^2+25x

Solución en video

Respuesta

c=0 c=0

Ejercicio #4

a = coeficiente de x²

b = coeficiente de x

c = coeficiente del número independiente


cuál es el valor de b b en la ecuación

y=4x2−16 y=4x^2-16

Solución en video

Respuesta

b=0 b=0

Ejercicio #5

a = coeficiente de x²

b = coeficiente de x

c = coeficiente del número independiente


cuál es el valor de c c en la ecuación

y=5+3x2 y=5+3x^2

Solución en video

Respuesta

c=5 c=5

Ejercicio 1

a = Coeficiente de x²

b = Coeficiente de x

c = Coeficiente del número independiente


cuál es el valor de \( b \) en la ecuación

\( y=3x^2+10-x \)

Ejercicio 2

a = Coeficiente de x²

b = Coeficiente de x

c = Coeficiente del número independiente


cuál es el valor de \( a \) en la ecuación

\( y=3x-10+5x^2 \)

Ejercicio 3

a = coeficiente de x²

b= coeficiente de x

c = coeficiente del número independiente

cuál es el valor de \( c \) en la ecuación

\( y=-5x^2+4x-3 \)

Ejercicio 4

a = coeficiente de x²

b = coeficiente de x

c = coeficiente del número independiente


cuál es el valor de \( b \) en la ecuación

\( y=2x-3x^2+1 \)

Ejercicio 5

a = coeficiente de x²

b = coeficiente de x

c = coeficiente del número independiente


cuál es el valor de \( a \) en la ecuación

\( y=-x^2-3x+1 \)

Ejercicio #6

a = Coeficiente de x²

b = Coeficiente de x

c = Coeficiente del número independiente


cuál es el valor de b b en la ecuación

y=3x2+10−x y=3x^2+10-x

Solución en video

Respuesta

b=−1 b=-1

Ejercicio #7

a = Coeficiente de x²

b = Coeficiente de x

c = Coeficiente del número independiente


cuál es el valor de a a en la ecuación

y=3x−10+5x2 y=3x-10+5x^2

Solución en video

Respuesta

a=5 a=5

Ejercicio #8

a = coeficiente de x²

b= coeficiente de x

c = coeficiente del número independiente

cuál es el valor de c c en la ecuación

y=−5x2+4x−3 y=-5x^2+4x-3

Solución en video

Respuesta

c=−3 c=-3

Ejercicio #9

a = coeficiente de x²

b = coeficiente de x

c = coeficiente del número independiente


cuál es el valor de b b en la ecuación

y=2x−3x2+1 y=2x-3x^2+1

Solución en video

Respuesta

b=2 b=2

Ejercicio #10

a = coeficiente de x²

b = coeficiente de x

c = coeficiente del número independiente


cuál es el valor de a a en la ecuación

y=−x2−3x+1 y=-x^2-3x+1

Solución en video

Respuesta

a=−1 a=-1

Ejercicio 1

Resuelva la siguiente ecuación

\( x^2+5x+4=0 \)

Ejercicio 2

Resuelva la siguiente ecuación

\( x^2+5x+6=0 \)

Ejercicio 3

Resuelva la siguiente ecuación

\( x^2-3x+2=0 \)

Ejercicio 4

Resuelva la siguiente ecuación

\( x^2-x-20=0 \)

Ejercicio 5

Resuelva la siguiente ecuación

\( x^2-4x+4=0 \)

Ejercicio #11

Resuelva la siguiente ecuación

x2+5x+4=0 x^2+5x+4=0

Solución en video

Respuesta

x1=−1,x2=−4 x_1=-1,x_2=-4

Ejercicio #12

Resuelva la siguiente ecuación

x2+5x+6=0 x^2+5x+6=0

Solución en video

Respuesta

x1=−3,x2=−2 x_1=-3,x_2=-2

Ejercicio #13

Resuelva la siguiente ecuación

x2−3x+2=0 x^2-3x+2=0

Solución en video

Respuesta

x1=1,x2=2 x_1=1,x_2=2

Ejercicio #14

Resuelva la siguiente ecuación

x2−x−20=0 x^2-x-20=0

Solución en video

Respuesta

x1=−4,x2=5 x_1=-4,x_2=5

Ejercicio #15

Resuelva la siguiente ecuación

x2−4x+4=0 x^2-4x+4=0

Solución en video

Respuesta

x=2 x=2

Temas que se aprenden en secciones posteriores

  1. Principales soluciones de una función cuadrática
  2. Trinomio al cuadrado
  3. Solución por extracción de raíz
  4. Completar el cuadrado en una ecuación cuadrática