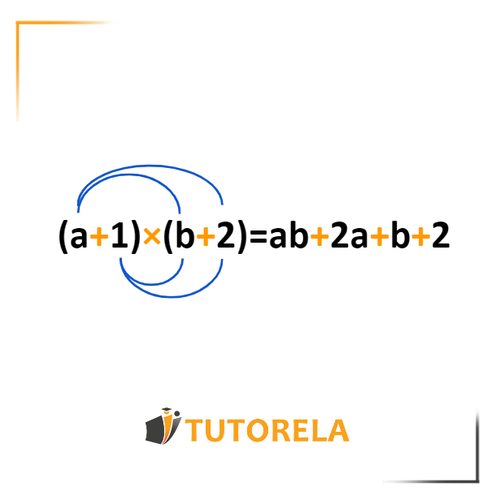
La propiedad distributiva extendida nos ayuda a resolver ejercicios con términos entre paréntesis que se multiplican por otros términos entre paréntesis.
Por ejemplo:
La solución de este tipo de ejercicios requiere que avancemos según los siguientes pasos:
- Paso 1: Multiplicar el primer término de los primeros paréntesis por cada uno de los términos de los segundos paréntesis.
- Paso 2: Multiplicar el segundo término de los primeros paréntesis por cada uno de los términos de los segundos paréntesis.
- Paso 3: Asociar términos semejantes.