Los alumnos comienzan a aprender matemáticas desde la primaria y, a medida que avanzan, la asignatura se va volviendo cada vez más complicada. Entre otros, el programa de estudios dedica una parte a la geometría y exige que los alumnos dominen las distintas formas y sepan cómo calcular su área y volumen. ¿Tú también estás estudiando estos días cómo calcular el volumen de un prisma rectangular?
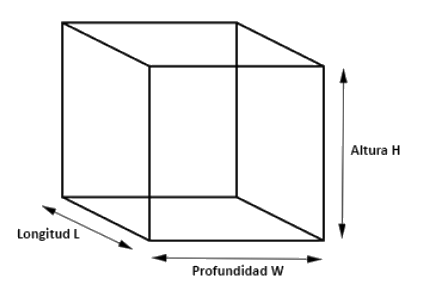
Volumen de un prisma rectangular:
V = largo × ancho × altura