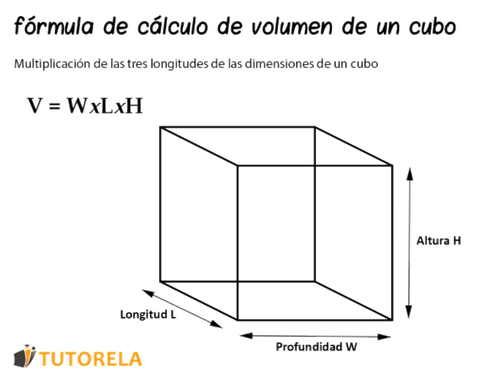
El cubo es un tipo de caja en el que las tres dimensiones (largo, ancho y altura) son idénticas.
Todos los cubos están compuestos por seis cuadrados idénticos.
Para calcular el volumen de un cubo debemos seguir los mismos pasos que para calcular el volumen de un ortoedro, es decir:
Longitud (L) × Profundidad (W) × altura (H).
Dado que el largo, el ancho y la altura son iguales, nos basta con saber uno de ellos para calcular el volumen del cubo.