Los Prismas rectangulares están compuestos por rectángulos distintos. Cuando te enfrentes a un ejercicio o un examen en el que te piden calcular el área de superficie de un Prisma rectangular, utiliza la fórmula que te indicamos a continuación.
Área Superficial de un Cuboide - Ejercicios y Problemas
Domina el cálculo del área superficial de cuboides con ejercicios paso a paso. Aprende fórmulas, resuelve problemas prácticos y mejora tus habilidades matemáticas.
- Calcular el área superficial de cualquier cuboide usando la fórmula correcta
- Identificar las dimensiones necesarias: largo, ancho y altura del cuboide
- Resolver problemas de la vida real con cajas, edificios y objetos rectangulares
- Aplicar unidades de medida correctas para áreas superficiales
- Descomponer figuras complejas en cuboides simples para calcular áreas totales
- Verificar respuestas usando diferentes métodos de cálculo del área superficial
Entendiendo la Área superficial del ortoedro
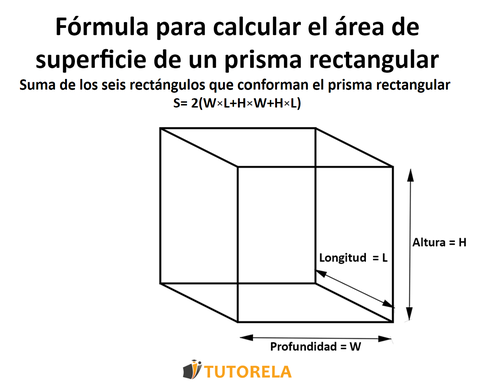
La fórmula: ¿cómo calcular el área de un prisma rectangular (ortoedro rectangular)?
S= área de superficie
Practicar Área superficial del ortoedro
Dado el ortoedro cuya base cuadrada es de tamaño 25 cm²,
La altura del ortoedro es 3 cm,
¿Cuál es la superficie del ortoedro?
ejemplos con soluciones para Área superficial del ortoedro
Dado el siguiente ortoedro
¿Cuál es la superficie?
Identificamos que las caras son
3*3, 3*11, 11*3
Como las caras opuestas de un ortoedro son iguales, sabemos que por cada cara que encontramos hay otra cara, por lo tanto:
3*3, 3*11, 11*3
o
(3*3, 3*11, 11*3 ) *2
Para hallar el área de la superficie, tendremos que sumar todas estas áreas, por lo tanto:
(3*3+3*11+11*3 )*2
¡Y esta es en realidad la fórmula para el área de superficie!
Calculamos:
(9+33+33)*2
(75)*2
150
Respuesta:
150
Dado un ortoedro cuyas dimensiones en el dibujo
¿Qué rectángulos forman el ortoedro?
Cada ortoedro, en realidad, esta compuesto de rectángulos, estos rectángulos son las caras del ortoedro.
Como sabemos que en un rectángulo las caras paralelas son iguales entre sí, podemos concluir que por cada cara encontrada habrá dos rectángulos.
Veamos primero la cara pintada de naranja,
Tiene ancho y alto, 5 y 3, entonces ya sabemos que son dos rectángulos de tamaño 5x6
Ahora veamos las caras de lado, también tienen una altura de 3, pero su ancho es de 6,
Y luego entendemos que hay dos rectángulos más de 3x6
Ahora veamos las caras superior e inferior, vemos que sus dimensiones son 5 y 6,
Por lo tanto, hay dos rectángulos más que tienen un tamaño de 5x6
Es decir, hay
2 rectángulos 5X6
2 rectángulos 3X5
2 rectángulos 6X3
Respuesta:
2 Rectángulos 5X6
2 Rectángulos 3X5
2 Rectángulos 6X3
Dado el siguiente ortoedro
¿Cuál es la superficie?
Primero, recordamos la fórmula para el área de superficie del ortoedro:
(ancho*largo + altura*ancho + altura*largo) *2
Como en el ortoedro, las caras opuestas son iguales entre sí, los datos existentes son suficientes para llegar a una solución.
Reemplazamos los datos en la fórmula:
(8*5+3*5+8*3) *2 =
(24+40+15) *2 =
79*2 =
158
Respuesta:
158
Dado el ortoedro de la figura:
¿Cuál es la superficie del ortoedro?
Recuerda que la fórmula del área superficial de un ortoedro es:
(largo X ancho + largo X altura + ancho X altura) 2
Colocamos los datos conocidos en la fórmula:
2*(3*2+2*5+3*5)
2*(6+10+15)
2*31 = 62
Respuesta:
62
Dado el ortoedro de la figura:
¿Cuál es la superficie del ortoedro?
Veamos qué rectángulos tenemos:
8*5
8*12
5*12
Recordemos la fórmula para la superficie de un ortoedro:
(largo X ancho + largo X altura + ancho X altura) 2
Ahora reemplazamos todo esto en el ejercicio:
(8*5+12*8+12*5)*2=
(40+60+96)*2=
196*2= 392
¡Esta es la solución!
Respuesta:
392 cm²