Ejercicios de Prisma Rectangular - Problemas de Ortoedro

Practica cálculo de volumen y área superficial de prismas rectangulares. Ejercicios resueltos paso a paso con ortoedros y cuboides para dominar geometría.

📚Domina los Prismas Rectangulares con Ejercicios Prácticos
  • Calcula volumen multiplicando largo, ancho y altura del prisma rectangular
  • Determina área superficial sumando las seis caras rectangulares del ortoedro
  • Resuelve problemas con incógnitas usando propiedades del prisma rectangular
  • Identifica caras, aristas y vértices en estructuras tridimensionales
  • Aplica fórmulas de volumen y superficie en situaciones del mundo real
  • Convierte entre diferentes unidades de medida en problemas de geometría

Entendiendo la Ortoedro

Explicación completa con ejemplos

Estructura de un prisma rectangular

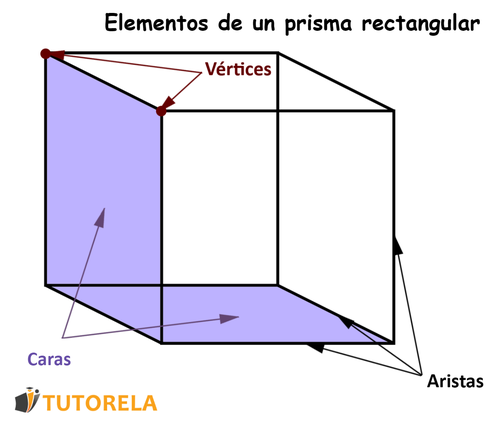
El prisma rectangular también llamado ortoedro, tiene una forma tridimensional y consta de seis rectángulos. Cada rectángulo se llama cara, por lo que cada prisma rectangular tiene seis caras (Dos caras opuestas también pueden llamarse bases del prisma rectangular). Es importante comprender que en realidad hay 33 pares de caras, y cada cara será exactamente igual a la cara ubicada frente a ella.

Las líneas rectas que se forman al intersecarse dos lados se denominan aristas. Cada prisma rectangular tiene 1212 aristas.

1a. Estructura de un prisma rectangular

Explicación completa

Practicar Ortoedro

Pon a prueba tus conocimientos con más de 64 cuestionarios

Dado el ortoedro:

888555121212

¿Cuál es el volumen del ortoedro?

ejemplos con soluciones para Ortoedro

Soluciones paso a paso incluidas
Ejercicio #1

Dado el ortoedro de la figura:

888555121212

¿Cuál es la superficie del ortoedro?

Solución Paso a Paso

Veamos qué rectángulos tenemos:

8*5

8*12

5*12

Recordemos la fórmula para la superficie de un ortoedro:

(largo X ancho + largo X altura + ancho X altura) 2

Ahora reemplazamos todo esto en el ejercicio:

(8*5+12*8+12*5)*2=
(40+60+96)*2=
196*2= 392

¡Esta es la solución!
 

Respuesta:

392 cm²

Solución en video
Ejercicio #2

Dado el ortoedro de la figura:

222333555

¿Cuál es la superficie del ortoedro?

Solución Paso a Paso

Recuerda que la fórmula del área superficial de un ortoedro es:

(largo X ancho + largo X altura + ancho X altura) 2

 

Colocamos los datos conocidos en la fórmula:

2*(3*2+2*5+3*5)

2*(6+10+15)

2*31 = 62

Respuesta:

62

Solución en video
Ejercicio #3

Dado el ortoedro cuyo largo es igual a 7 cm

El ancho es igual a 3 cm

La altura del ortoedro es igual a 5 cm

Calcule el volumen del cubo

333777555

Solución Paso a Paso

La fórmula para calcular el volumen de una ortoedro es:

altura*largo*ancho

Reemplazamos los datos en la fórmula:  

3*5*7

7*5 = 35

35*3 = 105

Respuesta:

105 cm³

Solución en video
Ejercicio #4

Dado el siguiente ortoedro

¿Cuál es la superficie?

333555888

Solución Paso a Paso

Primero, recordamos la fórmula para el área de superficie del ortoedro:

(ancho*largo + altura*ancho + altura*largo) *2

 

Como en el ortoedro, las caras opuestas son iguales entre sí, los datos existentes son suficientes para llegar a una solución.

Reemplazamos los datos en la fórmula:

 

(8*5+3*5+8*3) *2 =

(24+40+15) *2 =

79*2 = 

158

Respuesta:

158

Solución en video
Ejercicio #5

Dado el siguiente ortoedro

¿Cuál es la superficie?

333333111111

Solución Paso a Paso

Identificamos que las caras son

3*3, 3*11, 11*3
Como las caras opuestas de un ortoedro son iguales, sabemos que por cada cara que encontramos hay otra cara, por lo tanto:

3*3, 3*11, 11*3

o

(3*3, 3*11, 11*3 ) *2

 

Para hallar el área de la superficie, tendremos que sumar todas estas áreas, por lo tanto:

(3*3+3*11+11*3 )*2

 

¡Y esta es en realidad la fórmula para el área de superficie!

Calculamos:

(9+33+33)*2

(75)*2

150

Respuesta:

150

Solución en video

Preguntas Frecuentes

Todo lo que necesitas saber Ortoedro

¿Cómo calcular el volumen de un prisma rectangular paso a paso?

+
Para calcular el volumen de un prisma rectangular multiplica las tres dimensiones: Volumen = Largo × Ancho × Altura. Por ejemplo, si tienes un prisma de 4 cm de largo, 3 cm de ancho y 5 cm de altura: 4 × 3 × 5 = 60 cm³.

¿Cuál es la diferencia entre área superficial con y sin bases?

+
El área superficial sin bases incluye solo las 4 caras laterales: Ss = 2(W×H + L×H). El área total incluye las 6 caras: S = 2(W×L + H×W + H×L). La diferencia son las dos bases rectangulares del prisma.

¿Cuántas caras, aristas y vértices tiene un ortoedro?

+
Un ortoedro o prisma rectangular tiene: 1) 6 caras rectangulares, 2) 12 aristas donde se intersectan las caras, 3) 8 vértices en las esquinas. Estas características son constantes para todos los prismas rectangulares.

¿Qué nombres diferentes recibe el prisma rectangular?

+
El prisma rectangular puede llamarse: ortoedro, cuboide, prisma rectangular ortogonal, o simplemente cubo (cuando todas las dimensiones son iguales). Todos estos términos se refieren a la misma forma geométrica tridimensional.

¿Cómo resolver problemas de prisma rectangular con porcentajes?

+
Primero calcula cada dimensión usando los porcentajes dados: si el largo es 40% del ancho de 12 cm, entonces largo = (40 × 12) ÷ 100 = 4.8 cm. Luego aplica la fórmula correspondiente con los valores obtenidos.

¿Qué objetos cotidianos son prismas rectangulares?

+
Los prismas rectangulares están en todas partes: cajas de zapatos, CPU de computadoras, cajas de cereal, libros, ladrillos, y hasta las habitaciones de tu casa. Identificar estas formas ayuda a entender mejor la geometría tridimensional.

¿Cómo encontrar una dimensión faltante conociendo el volumen?

+
Si conoces el volumen y dos dimensiones, divide el volumen entre el producto de las dimensiones conocidas. Por ejemplo: si Volumen = 60 cm³, largo = 4 cm, ancho = 3 cm, entonces altura = 60 ÷ (4 × 3) = 5 cm.

¿Por qué las caras opuestas de un prisma rectangular son iguales?

+
Las caras opuestas son iguales porque un prisma rectangular se forma por tres pares de rectángulos paralelos. Cada par tiene las mismas dimensiones, por eso hay exactamente 3 pares de caras idénticas en total.

Practica por Tipo de Pregunta

Elige tu estilo de aprendizaje y formato de práctica preferido para problemas de fracciones
Aplicación de la fórmula Aumentando un elemento específico por adición de..... o multiplicación por....... Calcular el lado faltante basado en la fórmula Cálculo usando porcentajes ¿Cuántas veces cabe la forma dentro de otra forma? Datos con potencias y raíces Encontrar el área de la base en el perímetro y viceversa Identificar el valor mayor Problemas escritos Propiedad distributiva extendida Resta o suma a una forma más grande Sugiriendo opciones para términos cuando se conoce el resultado de la fórmula Una forma que consiste en varias formas (requiriendo la misma fórmula) Usando formas geométricas adicionales Uso de congruencia y semejanza Uso del Teorema de Pitágoras Uso de proporciones para el cálculo Uso de variables Aplicación de la fórmula Calcular el lado faltante basado en la fórmula Cálculo usando porcentajes ¿Cuántas veces cabe la forma dentro de otra forma? Encontrar el área de la base en el perímetro y viceversa Problemas escritos Resta o suma a una forma más grande Una forma que consiste en varias formas (requiriendo la misma fórmula) Uso del Teorema de Pitágoras Uso de proporciones para el cálculo Uso de variables Verificar si la fórmula es aplicable o no

Más Recursos y Enlaces

Explora más recursos y enlaces relacionados con Ortoedro
Practicar El cuboPracticar Cómo calcular el área de superficie de un prisma rectangular (ortoedro)Practicar Cómo calcular el volumen de un prisma rectangular (ortoedro)Practicar Partes de un ortoedro