Cada problema geométrico se basa en una gran cantidad de datos, cuya respuesta se divide en varias preguntas diferentes. Una de las preguntas más populares, y la más probable que aparezca en su prueba, es la pregunta sobre el área del rombo. Como es bien sabido, un rombo son triángulos diferentes. Si es así, ¿cómo se calcula su área?
Ejercicios de Área del Rombo - Práctica con Diagonales
Domina el cálculo del área del rombo con ejercicios paso a paso. Practica con fórmulas de diagonales, base × altura y problemas resueltos.
📚¿Qué aprenderás practicando área de rombo?
- Aplicar la fórmula área = (diagonal₁ × diagonal₂) ÷ 2
- Calcular área usando base × altura del rombo
- Resolver ejercicios con diagonales desconocidas usando Pitágoras
- Determinar longitudes de diagonales cuando se conoce el área
- Identificar cuando un rombo es un cuadrado especial
- Resolver problemas complejos con razones entre diagonales
Entendiendo la Área de un rombo
Explicación completa con ejemplos
¿Cómo se calcula el área de un rombo?
Formula del rombo
- La fórmula para calcular el área de un rombo: Diagonal Diagonal, dividido por .
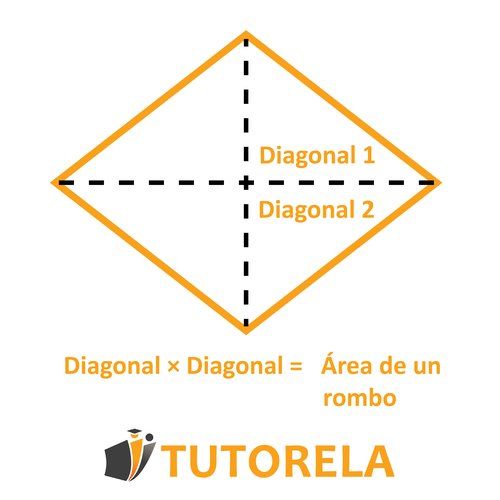
- Otra fórmula con la cual puedes pensar en el área del rombo (dependiendo de los datos que te proporcione la pregunta): Base Altura.
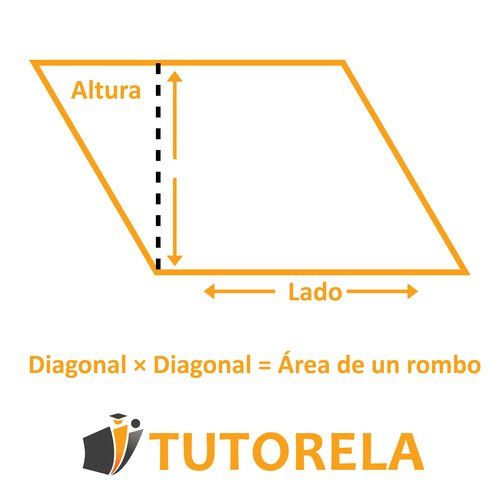
Practicar Área de un rombo
Pon a prueba tus conocimientos con más de 13 cuestionarios
Dado el rombo del dibujo y las longitudes de sus diagonales
¿Cuál es el área del rombo?
ejemplos con soluciones para Área de un rombo
Soluciones paso a paso incluidas
Ejercicio #1
Dado el rombo del dibujo:
¿Cuál es el área?
Solución Paso a Paso
Recordemos que el rombo tiene dos maneras de calcular su área:
La primera es lado por la altura del lado.
La segunda es diagonal por diagonal dividido 2.
Como nos dan las dos diagonales, lo calculamos de la segunda manera:
Respuesta:
14
Solución en video
Ejercicio #2
Dado el rombo de la figura
Halla su área:
Solución Paso a Paso
Primero, recordemos que de acuerdo con las propiedades del rombo, todos los lados de un rombo son iguales,
Por lo tanto, si definimos los lados del rombo con las letras ABCD,
Podemos argumentar que:
AB=BC=CD=DA
Usamos la fórmula del perímetro:
50 = AB+BC+CD+DA
Y podemos concluir que
4AB=50
(También podemos usar cualquier otro lado, no importa en este caso porque son todos iguales.)
Dividimos por cuatro y revelamos que:
AB=BC=CD=DA = 12.5
Ahora recordemos la fórmula para el área del rombo: la altura por el lado correspondiente a la altura.
Se nos da la longitud de la altura exterior 8,
Ahora, podemos reemplazar en la fórmula:
8*12.5=100
Respuesta:
100 cm²
Solución en video
Ejercicio #3
Dado el rombo del dibujo:
¿Cuál es el área?
Solución Paso a Paso
Recuerda que hay dos opciones para calcular el área de un rombo:
Diagonal por diagonal dividido 2.
Lado por la altura del lado.
En la pregunta se nos da solo la mitad de la diagonal y se nos da el lado, lo que significa que no podemos usar ninguna de las fórmulas.
Necesitamos encontrar más datos. Encontremos la segunda diagonal:
Recordemos que las diagonales de un rombo son perpendiculares entre sí, lo que significa que forman un ángulo de 90 grados.
Por lo tanto, todos los triángulos de un rombo son rectángulos.
Ahora podemos centrarnos en el triángulo donde están dados el lado y la altura, y calcularemos el tercer lado por el teorema de Pitágoras:
Reemplazamos los datos:
Ahora que hemos hallado la mitad de la segunda diagonal, podemos calcular el área mediante la diagonal por diagonal:
Dado que las diagonales en un rombo son perpendiculares y se cruzan entre sí, son iguales. Por lo tanto nuestras diagonales son iguales:
Por lo tanto, el área del rombo es:
Respuesta:
24
Solución en video
Ejercicio #4
Dado el rombo del dibujo:
¿Cuál es el área?
Solución Paso a Paso
Respuesta:
33
Solución en video
Ejercicio #5
Dado el rombo del dibujo cuya área es 24 cm²
¿Cuál es el valor de X?
Solución Paso a Paso
Respuesta:
6
Solución en video
Preguntas Frecuentes
¿Cuáles son las dos fórmulas principales para calcular el área de un rombo?
+Las dos fórmulas son: 1) Área = (diagonal₁ × diagonal₂) ÷ 2, y 2) Área = base × altura. La primera se usa cuando conoces las diagonales, la segunda cuando conoces un lado y la altura perpendicular.
¿Cómo encuentro una diagonal del rombo si solo conozco una diagonal y el área?
+Usa la fórmula del área despejando la diagonal desconocida: diagonal₂ = (2 × área) ÷ diagonal₁. Multiplica el área por 2 y divide entre la diagonal conocida.
¿Cuándo puedo usar el teorema de Pitágoras en problemas de área de rombo?
+Cuando te dan las medidas desde el centro hasta los vértices del rombo. Las diagonales se cortan perpendicularmente en el centro, formando triángulos rectángulos que puedes resolver con Pitágoras.
¿Qué diferencia hay entre calcular el área de un rombo y un cuadrado?
+Un cuadrado es un rombo especial con ángulos de 90°. Para el cuadrado usas lado², pero para un rombo general necesitas las diagonales o la altura, ya que sus ángulos no son rectos.
¿Cómo resuelvo ejercicios donde me dan la razón entre las diagonales del rombo?
+Primero establece las diagonales como múltiplos de la razón (ej: si es 3:2, sean 3x y 2x). Luego usa la fórmula del área para encontrar x, y finalmente calcula las diagonales reales.
¿Por qué divido entre 2 en la fórmula del área del rombo con diagonales?
+Porque el producto de las diagonales da el área de un rectángulo que contiene al rombo. El rombo ocupa exactamente la mitad de ese rectángulo, por eso se divide entre 2.
¿Qué errores comunes debo evitar al calcular el área del rombo?
+Los errores más comunes son: 1) Olvidar dividir entre 2 con las diagonales, 2) Confundir las semi-diagonales con las diagonales completas, y 3) No verificar que las medidas dadas sean realmente diagonales o lados.
¿Cómo verifico si mi respuesta del área del rombo es correcta?
+Puedes verificar usando la fórmula alternativa si tienes los datos. También revisa que las unidades sean correctas (área siempre en unidades cuadradas) y que el resultado sea lógicamente coherente con las dimensiones dadas.