Cada problema geométrico se basa en una gran cantidad de datos, cuya respuesta se divide en varias preguntas diferentes. Una de las preguntas más populares, y la más probable que aparezca en su prueba, es la pregunta sobre el área del rombo. Como es bien sabido, un rombo son triángulos diferentes. Si es así, ¿cómo se calcula su área?
El área de un rombo
¿Cómo se calcula el área de un rombo?
Formula del rombo
- La fórmula para calcular el área de un rombo: Diagonal Diagonal, dividido por .
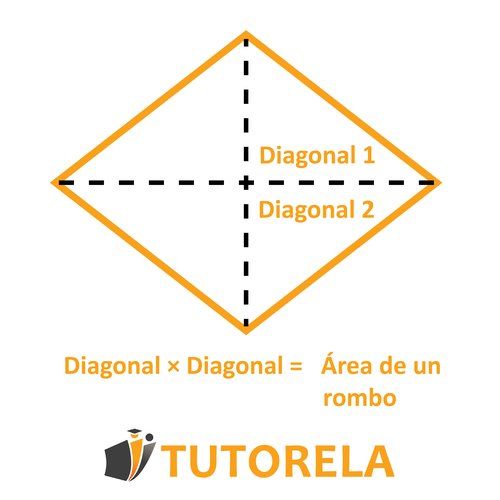
- Otra fórmula con la cual puedes pensar en el área del rombo (dependiendo de los datos que te proporcione la pregunta): Base Altura.
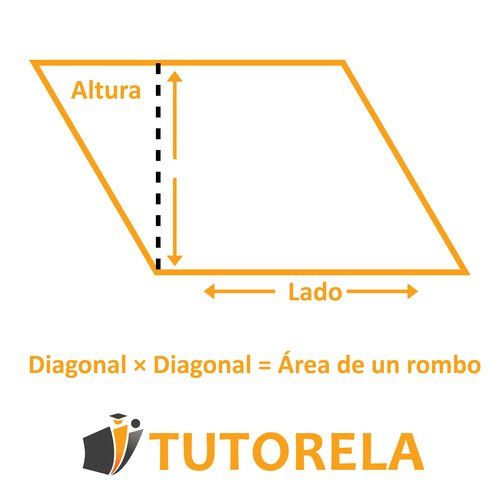
¡Pruébate en área de un rombo!
Dado el rombo de la figura
Calcula su área
La primera fórmula para calcular el área del rombo.
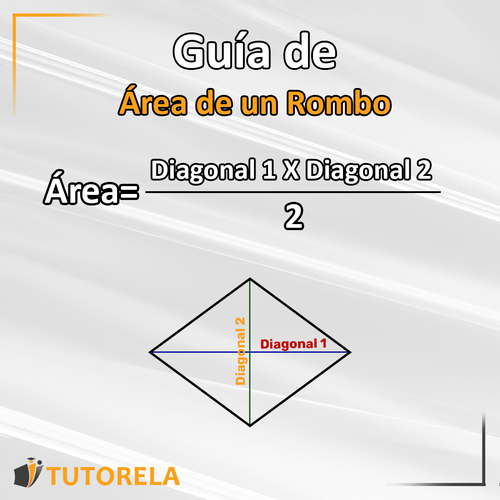
La segunda fórmula para calcular el área del rombo.
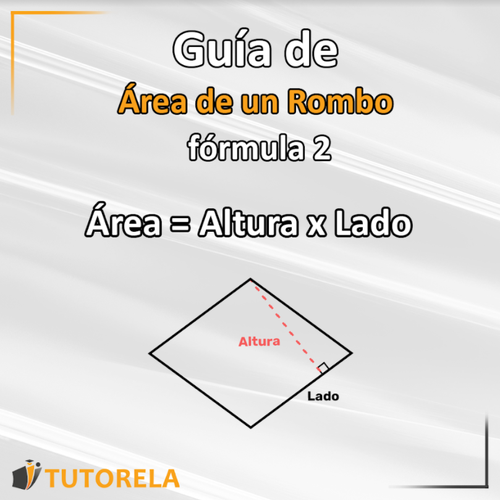
Ejemplo, cálculo de un área rombo
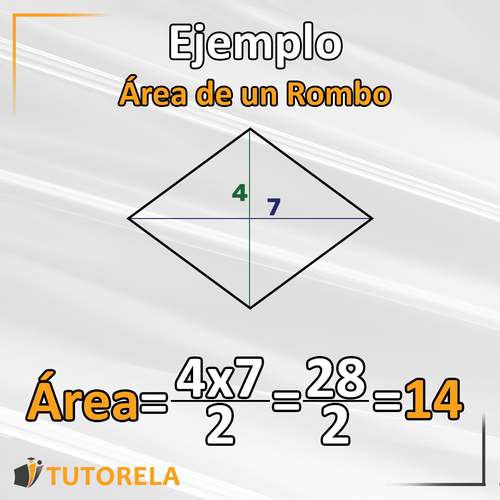
Dado el rombo del dibujo y las longitudes de sus diagonales
¿Cuál es el área del rombo?
En el dibujo dado un rombo
El largo de cada lado del rombo es 5 cm
La longitud de la altura del lado es 3 cm
¿Cuál es el área del rombo?
Dado el rombo del dibujo:
¿Cuál es el área?
Ejercicios de calculo de área de rombo
A continuación se presentan una variedad de ejercicios para calcular el área de rombo:
Ejemplo 1
- Diagonal
- Diagonal
Pregunta:
¿Cuál es el área del rombo?
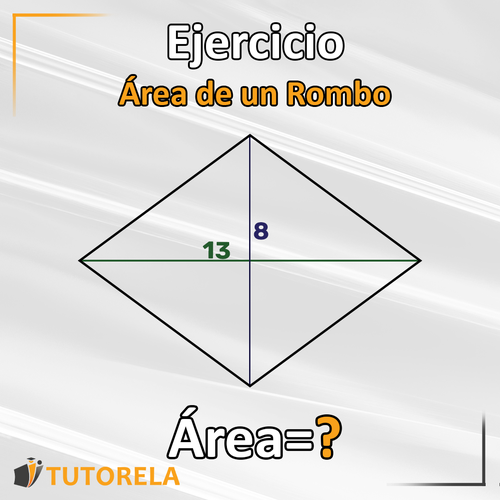
Explicación
El cálculo se hará de la siguiente manera: . Ahora, la cantidad debe dividirse por , y luego la respuesta obtenida es . Así que ustedes calcularán el área del rombo de acuerdo con los datos que se le presentarán en la pregunta.
Respuesta:
Dado el rombo de la figura
¿Cuál es su área?
Dado el rombo de la figura
¿Cuál es su área?
Dado el rombo del dibujo:
¿Cuál es el área?
Ejemplo 2
Diagonal
Diagonal
Pregunta:
¿Cuál es el área del rombo?
Explicación
El área del rombo .
Ahora dividimos este resultado por
Respuesta
El área del rombo es .
Otro ejemplo 3
Diagonal
Diagonal
Pregunta:
¿Cuál es el área del rombo?
Explicación
El área del rombo .
Posteriormente dividimos por
Respuesta
El área del rombo es entonces .
En el dibujo dado un rombo
La longitud de la diagonal principal 6 cm
La longitud de la diagonal secundaria 4 cm
¿Cuál es el área del rombo?
Dado el rombo de la figura
¿Cuál es el área?
Dado el rombo del dibujo y su altura exterior
El largo de cada lado del rombo es 5 cm
¿Cuál es su área?
Otro ejemplo 4
Cálculo del área del rombo según la fórmula de la base x Altura:
Base
Altura
Pregunta:
¿Cuál es el área del rombo?
Explicación
El área del rombo
Respuesta
El área del rombo es entonces .
Otro ejemplo 5
Cálculo del área del rombo según la fórmula de la base x Altura:
Base
Altura
Pregunta:
¿Cuál es el área del rombo?
Explicación
El área del rombo
Respuesta:
Dado el rombo del dibujo cuya área es 24 cm²
¿Cuál es el valor de X?
Dado el rombo cuya longitud de sus lados es 8 cm
La longitud de la altura dada es 5 cm
¿Cuál es el área del rombo?
Dado el rombo del dibujo:
¿Cuál es el área?
Ahora probaremos un ejercicio diferente
Pregunta:
Encuentra el valor de
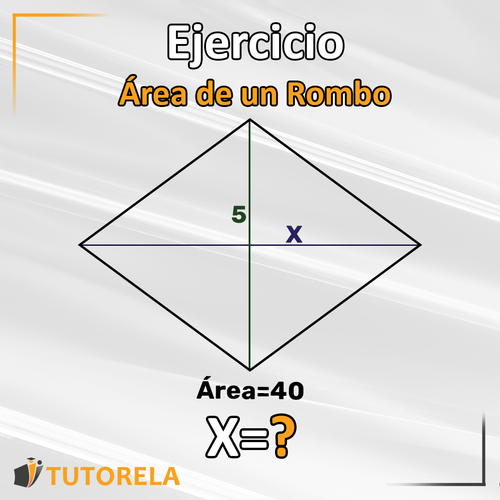
Explicación:
Para resolver el ejercicio, debemos utilizar la fórmula del área del rombo, y resolverlo "al revés".
Introduciremos los datos que conocemos en la fórmula:
Comenzaremos quitando del denominador, multiplicando la ecuación por .
Ahora, necesitamos despejar a la . Para ello dividimos la ecuación por .
Respuesta
El área del rombo es entonces .
Y ahora un ejercicio muy diferente
Pregunta:
¿Cuál es el área del rombo?
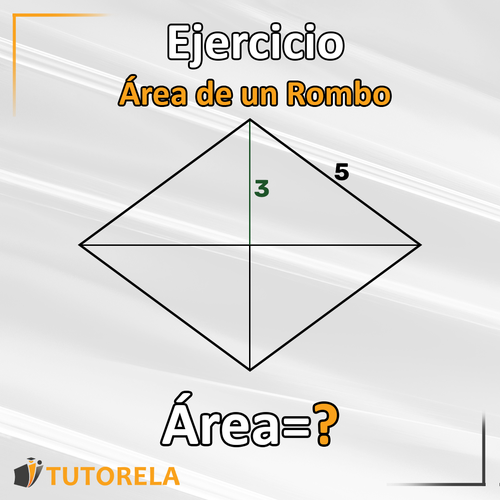
Explicación:
Para llegar a la solución, necesitaremos usar otra herramienta para llegar a la diagonal que falta.
Sabemos que las diagonales del rombo son perpendiculares entre sí y dividen el rombo en cuatro triángulos rectángulos.
Por lo tanto, podemos examinar nuestro triángulo y usar el teorema de Pitágoras para encontrar el lado que falta.
Introduciremos los datos que conocemos en el teorema de Pitágoras:
Ahora construiremos el ejercicio de acuerdo con las reglas, para despejar .
Ahora aplicaremos la raíz cuadrada de la ecuación para eliminar las potencias
¡Aún no hemos llegado a la solución del ejercicio!
Ahora que hemos encontrado el lado que falta, podemos usar la fórmula del área del rombo para encontrar su área.
(Diagonal A Diagonal B): 2
Es importante recordar que los datos que tenemos no son de todas las diagonales, sino solo desde el punto de intersección de las diagonales hasta los vértices.
Sabemos que las diagonales del rombo también se cortan entre sí, por lo tanto:
Diagonal
Diagonal
Ahora todo lo que queda es introducir los números en la fórmula y resolver:
Respuesta
el area es igual a
Si estás interesado en aprender a calcular áreas de otras formas geométricas puedes ingresar a uno de los siguientes artículos:
- ¿Cómo se calcula el área de un trapecio?
- Cómo calcular el área de un triángulo
- El área del paralelogramo: ¿qué es y cómo se calcula?
- Área circular
- Área de superficie de prismas triangulares
- ¿Cómo calcular el área de un hexágono regular?
- Área del rectángulo
- Cómo calcular el área de un ortoedro
- Diagonales de un rombo
- Simetría del rombo
- De paralelogramo a rombo
En la página web de Tutorela encontrarás una variedad de artículos sobre matemáticas.
Dado el rombo de la figura
El área es 66 cm²
¿Cuál es la longitud de la diagonal secundaria?
Dado el rombo de la figura
El área es igual a 35 cm²
¿Cuál es la longitud de la diagonal secundaria?
Dado el rombo de la figura
Calcula su área
Ejercicio resuelto del área de un rombo
Ejercicio resuelto 1 (Área del rombo )
Dado que el rombo de la gráfica tiene un área de
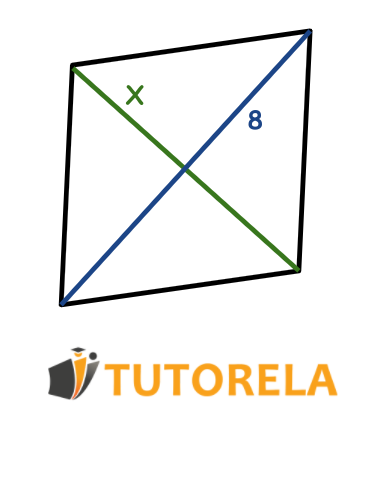
Tarea:
¿Cuál es el valor de ?
Fórmula del área del rombo
Pondremos los datos en la fórmula.
Ahora dividimos por
Ejercicio resuelto 2 (Área del rombo)
Encontrar las diagonales desde la fórmula:
Dado el dibujo del rombo, el área vale
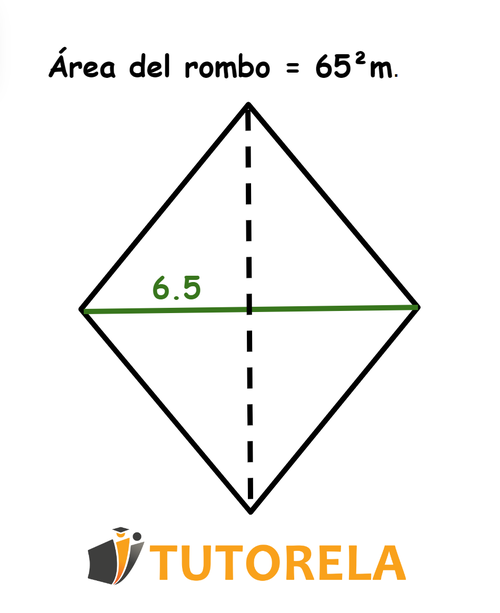
Tarea:
¿Cuál es la longitud de la diagonal principal en el rombo?
Solución:
La fórmula del área del rombo.
(Diagonal por Diagonal)/
Cuando el área es cm²
Colocaremos a, que es la diagonal principal y más larga entre las dos.
multiplicamos ambos lados por
Ahora dividimos por
Respuesta
La longitud de la diagonal principal en el rombo
Dado el rombo del dibujo y las longitudes de sus diagonales
¿Cuál es el área del rombo?
En el dibujo dado un rombo
El largo de cada lado del rombo es 5 cm
La longitud de la altura del lado es 3 cm
¿Cuál es el área del rombo?
Dado el rombo del dibujo:
¿Cuál es el área?
Ejercicio resuelto 3 (Área del rombo)
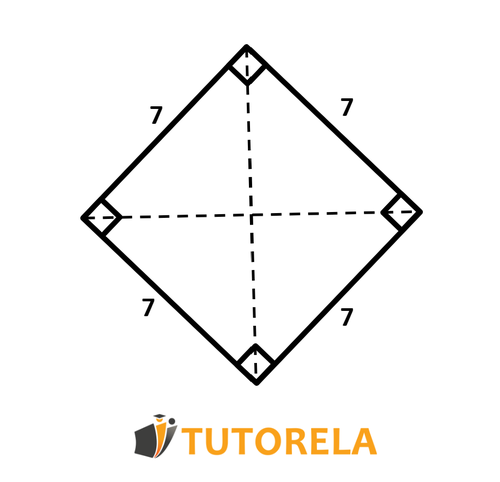
Tarea:
¿Cuál es el área del rombo?
Solución:
Un rombo cuyo par de ángulos adyacentes es igual a grados es un cuadrado,
Recuerda que un área de un cuadrado se puede calcular usando la fórmula:
Lado Lado = cuadrado
Pondremos los números en la fórmula y resolveremos
Respuesta:
El área del rombo o del cuadrado
Ejercicio resuelto 4
Dado el dibujo del rombo se tienen los siguentes datos como se muestra y
Tarea:
¿Cuál es el área del rombo?
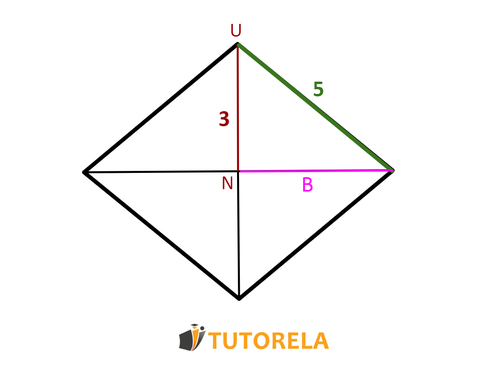
Solución:
Para encontrar la solución, necesitaremos usar otra herramienta para llegar a la diagonal que falta.
Sabemos que las diagonales del rombo son perpendiculares entre sí y dividen el rombo en cuatro triángulos rectángulos.
Por lo tanto, podemos mirar nuestro triángulo y usar el teorema de Pitágoras para encontrar el lado que falta.
Presentaremos los datos que conocemos en el teorema de Pitágoras:
Ahora moveremos los números para "aislar" el .
Aplicamos la raíz cuadrada de la ecuación para deshacerse de la potencia.
¡Esta, todavía no es la solución del ejercicio!
Ahora que hemos encontrado el lado que falta, podemos usar la fórmula del área del rombo para encontrar su área.
(Diagonal 1 Segunda Diagonal)
Es importante recordar que los datos que tenemos no son de todas las diagonales, sino solo desde el punto de vista de las diagonales a los vértices.
Sabemos que las diagonales del rombo también se cortan entre sí, por lo tanto
Diagonal 1
Diagonal 2
Ahora solo queda colocar en la fórmula y resolver:
Respuesta:
El Área es igual a
Dado el rombo de la figura
¿Cuál es su área?
Dado el rombo de la figura
¿Cuál es su área?
Dado el rombo del dibujo:
¿Cuál es el área?
Ejercicio resuelto 5
Dado el dibujo del rombo
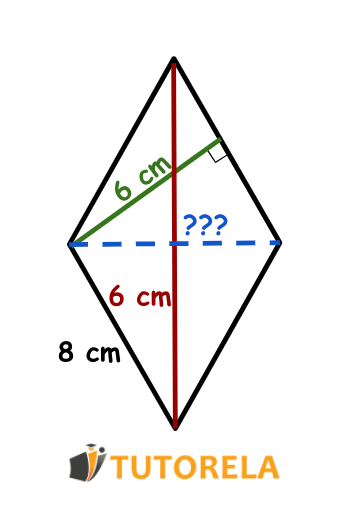
Pregunta:
¿Cuál es la longitud de la diagonal secundaria?
Solución:
Calcular el área del rombo
Área del rombo = lado X Altura
Es importante recordar que para calcular el área del rombo hay otra fórmula
Área del rombo = (Diagonal 1 Diagonal 2) /
multiplicamos por ( y son las diagonales)
; Dividimos ambos lados por
Introduciremos el área y la primera diagonal en la fórmula y resolveremos:
Respuesta:
La respuesta correcta es cm.
Ejercicio resuelto 6
Tema: Cálculo del rombo del área usando la relación
Dado el rombo en la figura:
Dado que la relación entre la longitud de la diagonal principal y la secundaria es
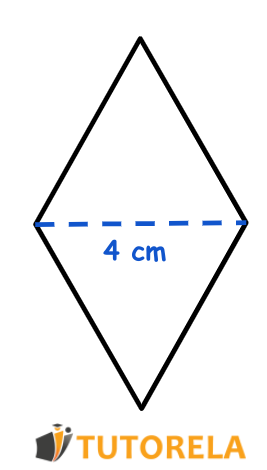
Tarea:
Encuentra el área del rombo
Solución:
Del dato que la relación entre las diagonales:
Diagonal1 / Diagonal2
En la figura dada en diagonal 2 (el que sea más corto) estableceremos su longitud en la fórmula que encontramos.
(Multiplicar en diagonal)
Lo dividiremos /
Calculemos el área del rombo:
Respuesta:
La respuesta es cm²
En el dibujo dado un rombo
La longitud de la diagonal principal 6 cm
La longitud de la diagonal secundaria 4 cm
¿Cuál es el área del rombo?
Dado el rombo de la figura
¿Cuál es el área?
Dado el rombo del dibujo y su altura exterior
El largo de cada lado del rombo es 5 cm
¿Cuál es su área?
¿Existe una fórmula definida para obtener un 100 en el examen?
La respuesta es sí y no. Por un lado, pueden prepararse para el examen de la mejor manera, pero aún así equivocarse en pequeños errores de cálculo (principalmente debido al estrés), que les provocará perder algunos puntos. Frente a ustedes, hay algunos consejos que colaboraran significativamente en sus posibilidades de obtener un en una prueba o examen de matemáticas. La clave del éxito: ¡perseverancia!
- Asistencia a clases de matemáticas en la escuela - ¡imprescindible! El autoaprendizaje no puede reemplazar el estudio del material por parte de sus maestros. En caso de haber faltado a una clase, asegúrese de completar el tema enseñado lo más rápido posible.
- Hacer los deberes consistentemente aumenta sus posibilidades de obtener excelencia. ¿Por qué? Debido a que la tarea le permite practicar con una variedad de ejercicios, enfrentar desafíos y comprender cuáles son sus errores comunes. También en la asignatura de matemáticas puede ser difícil en el entrenamiento, pero más fácil en la batalla (en el examen).
- Participación en la clase: ¡imprescindible! Cuanto más participe en la clase, mejor. ¿Por qué? Puesto que la participación te mantiene despierto e involucrado en el proceso de aprendizaje. Sugiera una solución a las preguntas que plantea el profesor y haga preguntas relevantes a los temas de estudio.
- Clase privada de matemáticas: ¡bienvenido! No importa cuál sea su nivel, sus calificaciones y la confianza que tenga en sí mismo. Las clases de refuerzo fortalecen sus bases, lo hacen avanzar tanto material como mentalmente y le permiten cosechar éxitos y calificaciones más altas.
- Planifique sus días de aprendizaje antes de la prueba con suficiente antelación. Prepare un tablero de tareas semanal, que detallará las horas de aprendizaje y los temas de aprendizaje. De esa manera, siempre llegarán listos para el examen e incluso podrán planificar un "día libre del estudio" el día anterior al examen. El objetivo: llegar a la prueba relajados, tranquilos y en paz.
Excelente consejo para el éxito en las matemáticas: ¡aprender de los ejemplos!
Como es sabido, muchas veces memorizan diferentes fórmulas. Por ejemplo: una fórmula para calcular el área rde un rombo. En lugar de memorizar una fórmula "vacía" sin datos, memorizamos una fórmula con datos. ¿Por qué? Porque este es un ejemplo de pregunta con respuesta, que puedes utilizar tanto en la preparación de los deberes como durante un examen. Cuando memorizan un ejemplo de cada tema tiene otro "ayuda interna" que lo asiste y le permite comprender mejor las preguntas adicionales.
Un ejemplo de cada tema es suficiente para "iluminarles el camino" y permitirle resolver preguntas de modo rápido y fácil. A veces, todo lo que necesita hacer es simplemente reemplazar los datos de la pregunta (como se indica en el examen), cuando por medio de la solución ya está bien integrada en su cabeza.
Dado el rombo del dibujo cuya área es 24 cm²
¿Cuál es el valor de X?
Dado el rombo cuya longitud de sus lados es 8 cm
La longitud de la altura dada es 5 cm
¿Cuál es el área del rombo?
Dado el rombo del dibujo:
¿Cuál es el área?
Lección privada de matemáticas, también para el fortalecimiento de las fórmulas.
No existe un estudiante que no sea bueno en matemáticas, pero existe un estudiante que no entiende las matemáticas. Muchas veces, lo que impide que los estudiantes obtengan buenas calificaciones no es su incapacidad, sino su falta de comprensión. Como es sabido, las lecciones en el plan de estudios de la escuela se llevan a cabo a un cierto ritmo, que no todos los estudiantes pueden seguir. De esta forma, las brechas se agrandan gradualmente y no se reducen.
Una clase de matemáticas privada puede fortalecer al estudiante y brindarle una caja de herramientas de calidad para continuar. A diferencia de las clases en un aula, la lección privada se centra únicamente en los puntos en los que el alumno se encuentra débil: desde la dificultad de entender lo que se le pide, hasta la dificultad de entender cómo aplicar las fórmulas en base a los datos presentados en la pregunta.
¡Una clase privada de matemáticas no indica debilidad!
Hay estudiantes que se sienten un poco avergonzados de contarles a sus compañeros sobre su intención de acortar las diferencias en una clase privada de matemáticas. En la práctica, realmente no hay motivo de vergüenza, todo lo contrario: los alumnos que vienen a una clase privada consiguen reforzar el material que se enseña en una clase extra. Muchas veces, el resultado es que los mismos estudiantes que estudian en la lección privada son en realidad más avanzados en el material que el resto de la clase. Las principales ventajas de la lección privada:
- Reducir las brechas: el alumno se compara con el ritmo de la clase.
- Asimilación del material aprendido en forma de "comprensión" y no de "memorización"
- Fortalecimiento de la confianza en sí mismo del alumno: ¡se demuestra a sí mismo que puede!
Dado el rombo de la figura
El área es 66 cm²
¿Cuál es la longitud de la diagonal secundaria?
Dado el rombo de la figura
El área es igual a 35 cm²
¿Cuál es la longitud de la diagonal secundaria?
Dado el rombo de la figura
Calcula su área
¿Cuántas lecciones privadas deberías tomar en matemáticas?
Ésta es una pregunta que no tiene una respuesta incuestionable. Algunos estudiantes están interesados en una reunión privada una vez a la semana. Sin embargo, hay estudiantes que se reúnen con un tutor privado justo antes de las pruebas, esto con el fin de reforzar fórmulas como cómo calcular un área de un rombo, crear simulaciones y desafiarse con preguntas más difíciles que las esperadas en la prueba.
Dado el rombo del dibujo y las longitudes de sus diagonales
¿Cuál es el área del rombo?
En el dibujo dado un rombo
El largo de cada lado del rombo es 5 cm
La longitud de la altura del lado es 3 cm
¿Cuál es el área del rombo?
Dado el rombo del dibujo:
¿Cuál es el área?
ejemplos con soluciones para Área de un rombo
Ejercicio #1
Dado el rombo del dibujo:
¿Cuál es el área?
Solución en video
Solución Paso a Paso
Recordemos que el rombo tiene dos maneras de calcular su área:
La primera es lado por la altura del lado.
La segunda es diagonal por diagonal dividido 2.
Como nos dan las dos diagonales, lo calculamos de la segunda manera:
Respuesta
14
Ejercicio #2
Dado el rombo de la figura
Halla su área:
Solución en video
Solución Paso a Paso
Primero, recordemos que de acuerdo con las propiedades del rombo, todos los lados de un rombo son iguales,
Por lo tanto, si definimos los lados del rombo con las letras ABCD,
Podemos argumentar que:
AB=BC=CD=DA
Usamos la fórmula del perímetro:
50 = AB+BC+CD+DA
Y podemos concluir que
4AB=50
(También podemos usar cualquier otro lado, no importa en este caso porque son todos iguales.)
Dividimos por cuatro y revelamos que:
AB=BC=CD=DA = 12.5
Ahora recordemos la fórmula para el área del rombo: la altura por el lado correspondiente a la altura.
Se nos da la longitud de la altura exterior 8,
Ahora, podemos reemplazar en la fórmula:
8*12.5=100
Respuesta
100 cm²
Ejercicio #3
Dado el rombo del dibujo:
¿Cuál es el área?
Solución en video
Solución Paso a Paso
Recuerda que hay dos opciones para calcular el área de un rombo:
Diagonal por diagonal dividido 2.
Lado por la altura del lado.
En la pregunta se nos da solo la mitad de la diagonal y se nos da el lado, lo que significa que no podemos usar ninguna de las fórmulas.
Necesitamos encontrar más datos. Encontremos la segunda diagonal:
Recordemos que las diagonales de un rombo son perpendiculares entre sí, lo que significa que forman un ángulo de 90 grados.
Por lo tanto, todos los triángulos de un rombo son rectángulos.
Ahora podemos centrarnos en el triángulo donde están dados el lado y la altura, y calcularemos el tercer lado por el teorema de Pitágoras:
Reemplazamos los datos:
Ahora que hemos hallado la mitad de la segunda diagonal, podemos calcular el área mediante la diagonal por diagonal:
Dado que las diagonales en un rombo son perpendiculares y se cruzan entre sí, son iguales. Por lo tanto nuestras diagonales son iguales:
Por lo tanto, el área del rombo es:
Respuesta
24
Ejercicio #4
Dado el rombo de la figura
Calcula su área
Solución en video
Respuesta
10 cm²
Ejercicio #5
Dado el rombo del dibujo y las longitudes de sus diagonales
¿Cuál es el área del rombo?
Solución en video
Respuesta
7.5 cm²
- Deltoide
- Área del deltoide:
- Paralelogramo
- El área del paralelogramo: ¿qué es y cómo se calcula?
- Perímetro de un paralelogramo
- Maneras de identificar paralelogramos
- Simetría rotacional en paralelogramos
- Del cuadrilátero al paralelogramo
- Trapecios
- Simetría en trapecios
- Diagonales de un trapecio isósceles
- Área de un trapecio
- Perímetro de un trapecio
- Trapecio isósceles
- Rectángulo
- De un cuadrilátero a un rectángulo
- Del paralelogramo al rectángulo
- ¿Cómo se calcula el área de un rectángulo?
- El perímetro del rectángulo
- Rectángulos congruentes
- Cuadrado
- El área de un cuadrado
- De paralelogramo a cuadrado
- Área
- ¿Rombo, cometa o diamante?
- Diagonales de un rombo
- Simetría del rombo
- De paralelogramo a rombo
- El área de un rombo
- Perímetro
- Áreas de Polígonos para 7º Grado
- Área de un trapecio rectángulo
- Área de un trapecio isósceles
- ¿Cómo calculamos el área de figuras complejas?
- ¿Cómo calculamos el perímetro de los polígonos?
- Orden de operaciones básicas: suma, resta, multiplicación y división
- Orden de las operaciones básicas (potencias)
- Orden de operaciones básicas: raíces
- El 0 y el 1 en el orden de las operaciones
- Inverso multiplicativo
- Orden de las operaciones: paréntesis
- La propiedad conmutativa
- La propiedad asociativa
- Cómo calcular el área de un ortoedro
- Potenciación de números enteros
- Las Tablas de Multiplicar
- Fracciones









