¿Cómo se llama? ¿Rombo, cometa o diamante? ;)
¿Rombo, cometa o diamante?
¿Rombo, cometa o diamante? Las propiedades, las fórmulas y absolutamente todo lo que debes saber
Entre nosotros... no tiene importancia. Se trata de aquella figura geométrica misteriosa que nos recuerda un diamante precioso o un juego de naipes... La llames como la llames, deberás conocer las propiedades de esta figura y su singularidad para superar ciertas problemáticas geométricas. Así que, comencemos...

¡Pruébate en rombo!
Dado el rombo de la figura
Calcula su área
Definiciones del rombo
El rombo es un polígono de cuatro lados de igual longitud. Si hablamos de la «familia extensa» podemos admitir que un rombo es, de hecho, un caso particular de las figuras deltoide y paralelogramo. Por otro lado, si un cierto rombo se caracteriza por tener también cuatro ángulos equivalentes (es decir, cada uno de 90º) el rombo pasa a ser un cuadrado.
Propiedades del rombo
A continuación, se exponen las principales características que describen al rombo. Para poder explicarlas de un modo claro haremos uso de la siguiente ilustración:
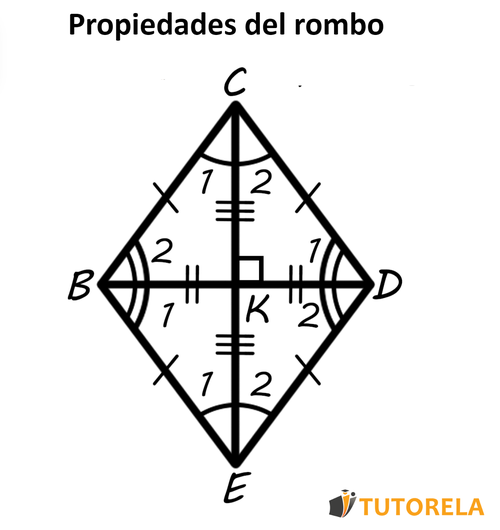
- Todos los lados del rombo tienen la misma longitud. Es decir, se cumple
- Los lados opuestos del rombo son paralelos. Es decir, se cumple :
- Los ángulos opuestos del rombo tienen la misma amplitud. Es decir, se cumple:
- Si se baja altura a cada lado, las cuatro tendrán el mismo largo. En la ilustración se ve una altura sola que desciende del vértice al lado .
- Se puede inscribir un círculo en cualquier rombo.
- En todo rombo hay dos diagonales perpendiculares. Es decir, se cumple: es vertical a .
- El punto de encuentro de las dos diagonales divide a cada diagonal en dos partes iguales. Es decir, se cumple:
- Cada diagonal divide los ángulos del rombo en dos ángulos iguales. Es decir, se cumple:
Dado el rombo del dibujo y las longitudes de sus diagonales
¿Cuál es el área del rombo?
En el dibujo dado un rombo
El largo de cada lado del rombo es 5 cm
La longitud de la altura del lado es 3 cm
¿Cuál es el área del rombo?
Dado el rombo del dibujo:
¿Cuál es el área?
Demostración del rombo
Para demostrar que un cuadrilátero es un rombo podemos utilizar el modo directo o indirecto. Si optamos por el modo directo, deberemos demostrar que los cuatro lados de dicho cuadrilátero tienen la misma longitud. Utilizando el modo indirecto debemos demostrar primeramente que el polígono es un paralelogramo. Luego de haber conseguido demostrar que cierto cuadrilátero es un paralelogramo nos quedan tres opciones:
- Demostrar que las diagonales del paralelogramo actúan como bisectrices
- Demostrar que las diagonales del paralelogramo son perpendiculares
- Demostrar que los dos lados contiguos del paralelogramo son equivalentes
Según los datos que haya en el ejercicio podremos elegir el modo más adecuado para actuar y así demostrar que cierto paralelogramo es, de hecho, un rombo.
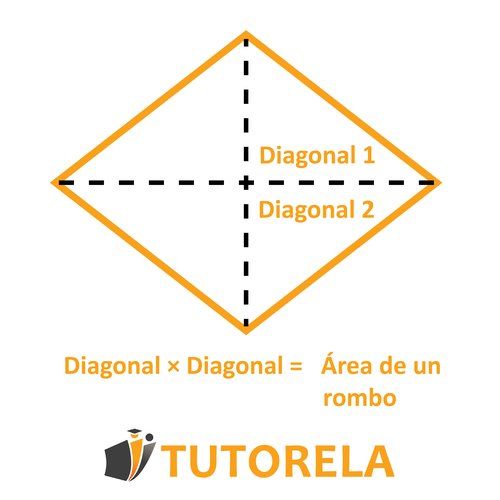
Fórmula para calcular el área de un rombo
Hay varias formas de calcular el área de un rombo. En esta sección mencionaremos brevemente dos fórmulas para calcular el área del rombo. Si quieres ampliar los conocimientos al respecto te invitamos a leer el artículo completo sobre el tema del área del rombo.
Para verlo de un modo simple, también en este caso, nos basaremos en la siguiente ilustración:
Dado el rombo de la figura
¿Cuál es su área?
Dado el rombo de la figura
¿Cuál es su área?
Dado el rombo del dibujo:
¿Cuál es el área?
Modo A
Se multiplican las longitudes de las diagonales y se divide por .
Es decir, se cumple:
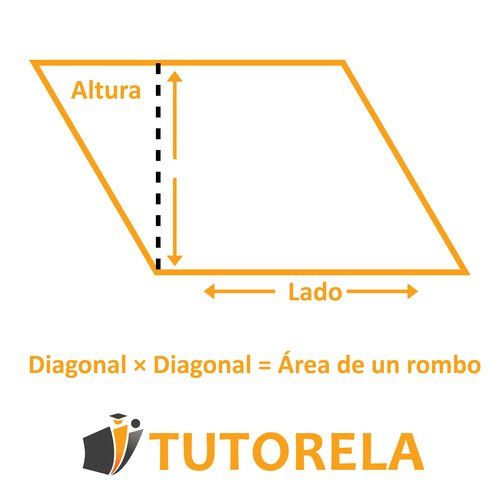
Modo B
Se multiplica uno de los lados por la altura.
Es decir, se cumple:
En el dibujo dado un rombo
La longitud de la diagonal principal 6 cm
La longitud de la diagonal secundaria 4 cm
¿Cuál es el área del rombo?
Dado el rombo de la figura
¿Cuál es el área?
Dado el rombo del dibujo y su altura exterior
El largo de cada lado del rombo es 5 cm
¿Cuál es su área?
Cálculo del perímetro de un rombo
Hemos llegado a la parte más sencilla de todas, que es el cálculo del perímetro de un rombo. Recordemos que, el perímetro de un rombo consiste en la suma de las longitudes de sus lados.
Debido a que los cuatro lados del rombo tienen la misma longitud, nos alcanza con saber sólo la de uno. A continuación, multiplicaremos la longitud de un lado por y obtendremos el perímetro del rombo.
Ejemplos y ejercitación sobre la demostración del rombo
Ejercicio No 1
Dado el rombo .
Uno de los ángulos dados Acorde a los datos de la ilustración halla los tres ángulos restantes del rombo.
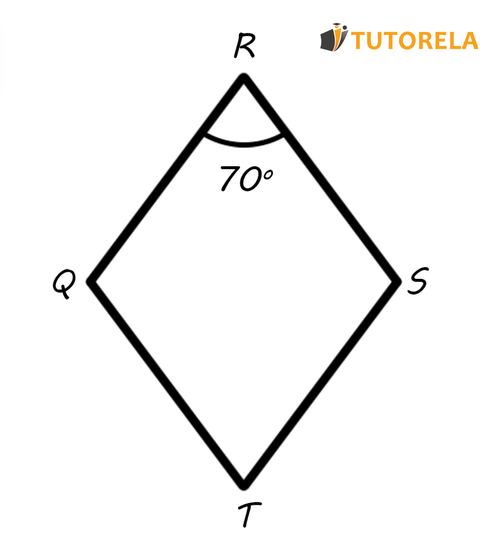
Solución:
Enfoquémonos en el dato dado. Sabemos el ángulo del vértice que equivale a
Acorde a lo que sabemos sobre las propiedades del rombo, los ángulos opuestos tienen la misma amplitud, por lo tanto, también el ángulo del vértice equivaldrá a .
El rombo es un cuadrilátero, por consiguiente, la suma de todos sus ángulos es grados, obtendremos que la suma de los ángulos y es: .
Recordemos nuevamente que, los ángulos opuestos del rombo tienen la misma amplitud. De esto deriva que, cada uno de los ángulos de los vértices restantes, y , medirá .
Respuesta: los ángulos del rombo son
Dado el rombo del dibujo cuya área es 24 cm²
¿Cuál es el valor de X?
Dado el rombo cuya longitud de sus lados es 8 cm
La longitud de la altura dada es 5 cm
¿Cuál es el área del rombo?
Dado el rombo de la figura, ¿Cuáles son los ángulos marcados?
Ejercicio No 2
Dado el rombo .
Acorde a los datos de la ilustración halla el perímetro y el área del rombo.
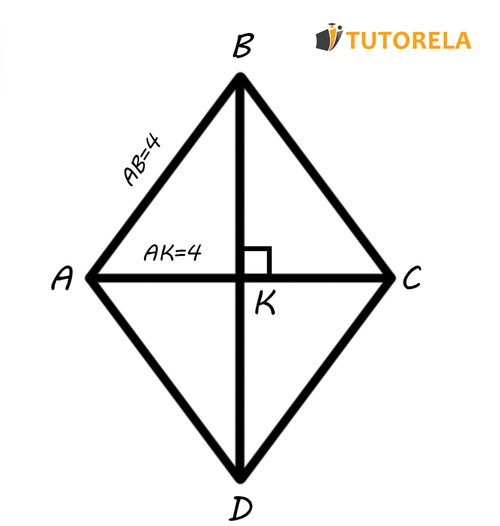
Solución:
Primero observaremos el esquema. Conocemos uno de los lados del rombo. Acorde a las propiedades que hemos aprendido, los cuatro ángulos del rombo son equivalentes.
Por lo tanto, se cumple: .
El perímetro del rombo es la suma de sus cuatro lados, por consiguiente, multiplicaremos por y nos dará cm.
Ahora pasemos a calcular el área del rombo. Para hacerlo elegiremos la primera opción que estudiamos, es decir, multiplicaremos las diagonales y dividiremos por .
En la ilustración se puede ver que . Conforme a las propiedades del rombo el punto de intersección de las diagonales del rombo las cruza, por lo cual se llega a que . Sólo nos queda hallar la segunda diagonal.
Recordemos otra característica del rombo: las diagonales del rombo son perpendiculares. Es decir, el triángulo es un triángulo rectángulo al cual es aplicable el teorema de Pitágoras. Basándonos en el teorema de Pitágoras calcularemos .
Se cumple:
Nuevamente, las diagonales se intersecan y, por lo tanto: .
Es decir, se cumple:
Respuesta:
El perímetro del rombo es Cm.
El área del rombo es Cm.
Ejemplos y ejercicios con soluciones de rombo
Ejercicio #1
Dado el rombo de la figura, ¿Cuáles son los ángulos marcados?
Solución Paso a Paso
Recordemos las diferentes definiciones de los ángulos:
Los ángulos correspondientes son ángulos situados en el mismo lado de la recta que corta a las dos paralelas y también están situados en el mismo nivel con respecto a la recta paralela a la que son adyacentes.
Por lo tanto, según esta definición, estos son los ángulos marcados con la letra A
Los ángulos alternos son ángulos situados en dos lados distintos de la recta que corta a dos paralelas, y que tampoco están al mismo nivel con respecto a la paralela a la que son adyacentes.
Por lo tanto, según esta definición, estos son los ángulos marcados con la letra B
Respuesta
A- correspondientes B- alternos
Ejercicio #2
Dado el rombo del dibujo:
¿Cuál es el área?
Solución en video
Solución Paso a Paso
Recordemos que el rombo tiene dos maneras de calcular su área:
La primera es lado por la altura del lado.
La segunda es diagonal por diagonal dividido 2.
Como nos dan las dos diagonales, lo calculamos de la segunda manera:
Respuesta
14
Ejercicio #3
Dado el rombo de la figura
Halla su área:
Solución en video
Solución Paso a Paso
Primero, recordemos que de acuerdo con las propiedades del rombo, todos los lados de un rombo son iguales,
Por lo tanto, si definimos los lados del rombo con las letras ABCD,
Podemos argumentar que:
AB=BC=CD=DA
Usamos la fórmula del perímetro:
50 = AB+BC+CD+DA
Y podemos concluir que
4AB=50
(También podemos usar cualquier otro lado, no importa en este caso porque son todos iguales.)
Dividimos por cuatro y revelamos que:
AB=BC=CD=DA = 12.5
Ahora recordemos la fórmula para el área del rombo: la altura por el lado correspondiente a la altura.
Se nos da la longitud de la altura exterior 8,
Ahora, podemos reemplazar en la fórmula:
8*12.5=100
Respuesta
100 cm²
Ejercicio #4
Dado el rombo del dibujo:
¿Cuál es el área?
Solución en video
Solución Paso a Paso
Recuerda que hay dos opciones para calcular el área de un rombo:
Diagonal por diagonal dividido 2.
Lado por la altura del lado.
En la pregunta se nos da solo la mitad de la diagonal y se nos da el lado, lo que significa que no podemos usar ninguna de las fórmulas.
Necesitamos encontrar más datos. Encontremos la segunda diagonal:
Recordemos que las diagonales de un rombo son perpendiculares entre sí, lo que significa que forman un ángulo de 90 grados.
Por lo tanto, todos los triángulos de un rombo son rectángulos.
Ahora podemos centrarnos en el triángulo donde están dados el lado y la altura, y calcularemos el tercer lado por el teorema de Pitágoras:
Reemplazamos los datos:
Ahora que hemos hallado la mitad de la segunda diagonal, podemos calcular el área mediante la diagonal por diagonal:
Dado que las diagonales en un rombo son perpendiculares y se cruzan entre sí, son iguales. Por lo tanto nuestras diagonales son iguales:
Por lo tanto, el área del rombo es:
Respuesta
24
Ejercicio #5
Dado el rombo de la figura
Calcula su área
Solución en video
Respuesta
10 cm²
Dado el rombo del dibujo:
¿Cuál es el área?
Dado el rombo de la figura
El área es 66 cm²
¿Cuál es la longitud de la diagonal secundaria?
Dado el rombo de la figura
Calcula su área
- Altura del triángulo
- Deltoide
- Área del deltoide:
- Suma de los ángulos internos de un triángulo
- Los lados o aristas de un triángulo
- Paralelogramo
- El área del paralelogramo: ¿qué es y cómo se calcula?
- Perímetro de un paralelogramo
- Maneras de identificar paralelogramos
- Simetría rotacional en paralelogramos
- Del cuadrilátero al paralelogramo
- Trapecios
- Simetría en trapecios
- Diagonales de un trapecio isósceles
- Área de un trapecio
- Perímetro de un trapecio
- Trapecio isósceles
- Rectángulo
- De un cuadrilátero a un rectángulo
- Del paralelogramo al rectángulo
- ¿Cómo se calcula el área de un rectángulo?
- El perímetro del rectángulo
- Rectángulos congruentes
- Ángulo exterior de un triángulo
- Cuadrado
- El área de un cuadrado
- De paralelogramo a cuadrado
- Área
- ¿Rombo, cometa o diamante?
- Diagonales de un rombo
- Simetría del rombo
- De paralelogramo a rombo
- El área de un rombo
- Perímetro
- Triángulo
- Tipos de triángulos
- Triángulo obtuso
- Triángulo equilátero
- Identificación de un triángulo isósceles
- Triángulo escaleno
- Triángulo agudo
- Triángulo isósceles
- Área de un triángulo
- Área de un triángulo rectángulo
- Área del triángulo isósceles
- Área del triángulo escaleno
- Área del triángulo equilátero
- Perímetro de un triángulo
- Áreas de Polígonos para 7º Grado
- Triángulo Rectángulo
- Área de un trapecio rectángulo
- Área de un trapecio isósceles
- Mediana en un triángulo
- Centro de un Triángulo - El Centroide - El Punto de Intersección de las Medianas
- ¿Cómo calculamos el área de figuras complejas?
- ¿Cómo calculamos el perímetro de los polígonos?
- Todos los términos en el cálculo de triángulos
- ¿Cómo calcular el área de un triángulo usando trigonometría?
- Orden de operaciones básicas: suma, resta, multiplicación y división
- Orden de las operaciones básicas (potencias)
- Orden de operaciones básicas: raíces
- El 0 y el 1 en el orden de las operaciones
- Inverso multiplicativo
- Orden de las operaciones: paréntesis
- La propiedad conmutativa
- La propiedad asociativa
- Cómo calcular el área de un ortoedro
- Potenciación de números enteros
- Las Tablas de Multiplicar
- Fracciones









