Entonces, ¿cómo convertimos una fracción simple a una fracción decimal? Primero, podemos tranquilizarte diciendo que la respuesta es: bastante fácil. Todo lo que necesitas es entender la técnica, y principalmente entender el significado de la fracción decimal. Primero, ¿cómo se ven las fracciones decimales? Aparecen en la siguiente forma: 0.5, 3.6, y así sucesivamente. O en otras palabras: "la fracción con el punto".
Ejercicios de Conversión de Decimales a Fracciones
Practica la conversión de números decimales a fracciones simples y números mixtos. Ejercicios paso a paso con soluciones detalladas.
📚¿Qué vas a aprender en esta práctica?
- Convertir decimales como 0.5, 0.25 y 0.125 a fracciones simples
- Simplificar fracciones decimales usando denominadores 10, 100 y 1000
- Transformar decimales periódicos en fracciones equivalentes
- Identificar el denominador correcto para cada tipo de decimal
- Resolver ejercicios de decimales a números mixtos paso a paso
- Verificar conversiones usando la división de numerador entre denominador
Entendiendo la Conversión de fracciones decimales en simples y mixtas
Explicación completa con ejemplos
Convertir una fracción simple a decimal - ¿cómo calcular?
De hecho, hay un punto que crea el límite entre el número entero y la fracción. Para convertir una fracción simple a una fracción decimal, necesitas elegir un denominador: 10, 100 o 1000. Entonces, ¿cómo puedes también convertir fracciones "simples" a fracciones decimales? Presta atención:
Datos básicos de fracciones:
- La línea que separa dos números diferentes se llama línea de fracción.
- La parte superior de la fracción - numerador.
- La parte inferior de la fracción - denominador.
Ten en cuenta que cuando convertimos una fracción "clásica" simple a una fracción decimal, la línea de fracción desaparece y un punto decimal separa los números.
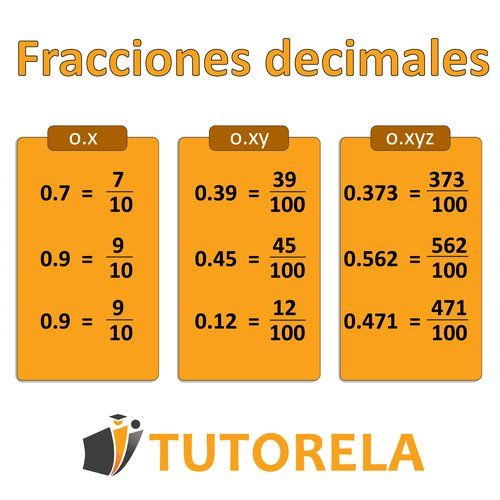
Practicar Conversión de fracciones decimales en simples y mixtas
Pon a prueba tus conocimientos con más de 58 cuestionarios
Elija la fracción decimal adecuada:
\( \frac{13}{100}= \)
ejemplos con soluciones para Conversión de fracciones decimales en simples y mixtas
Soluciones paso a paso incluidas
Ejercicio #1
Elija la fracción decimal adecuada:
Solución Paso a Paso
Escribe la fracción simple en forma decimal
Como la fracción está dividida por 10, movemos el punto decimal un lugar a la izquierda y obtenemos:
Agregamos el cero a la izquierda del punto decimal y obtenemos:
Respuesta:
0.5
Solución en video
Ejercicio #2
Elija la fracción decimal adecuada:
Solución Paso a Paso
Escribe la fracción simple en forma decimal
Como la fracción es divisible por 10, movemos el punto decimal un lugar a la izquierda y obtenemos:
Agreguemos el cero a la izquierda del punto decimal y obtenemos:
Respuesta:
0.7
Solución en video
Ejercicio #3
Solución Paso a Paso
Prestemos atención a dónde está ubicado el punto decimal en el número.
Recuerda:
Un número después del punto decimal representa décimas
Dos números después del punto decimal representan centésimas
Tres números después del punto decimal representan milésimas
Y así sucesivamente
En este caso hay tres números después del punto decimal, por lo que el número se divide entre 1000
Escribe la fracción de la siguiente manera:
Eliminamos los ceros extra y obtenemos:
Respuesta:
Solución en video
Ejercicio #4
Elija la fracción decimal adecuada:
Solución Paso a Paso
Respuesta:
0.02
Solución en video
Ejercicio #5
Elija la fracción decimal adecuada:
Solución Paso a Paso
Respuesta:
0.03
Solución en video
Preguntas Frecuentes
¿Cómo convertir 0.5 a fracción?
+Para convertir 0.5 a fracción, coloca 5 como numerador y 10 como denominador (5/10). Luego simplifica dividiendo ambos números por su máximo común divisor, que es 5. El resultado es 1/2.
¿Cuál es la diferencia entre convertir 0.2 y 0.25 a fracción?
+0.2 tiene una cifra decimal, por lo que se convierte a 2/10 = 1/5. En cambio, 0.25 tiene dos cifras decimales, por lo que se convierte a 25/100 = 1/4. El denominador depende del número de cifras decimales.
¿Qué denominador usar para convertir decimales a fracciones?
+El denominador debe ser: 10 para una cifra decimal (0.3 = 3/10), 100 para dos cifras (0.37 = 37/100), 1000 para tres cifras (0.125 = 125/1000), y así sucesivamente.
¿Cómo simplificar una fracción decimal como 25/100?
+Para simplificar 25/100, encuentra el máximo común divisor de 25 y 100, que es 25. Divide ambos números: 25÷25 = 1 y 100÷25 = 4. La fracción simplificada es 1/4.
¿Cuáles son los pasos para convertir 1.75 a número mixto?
+Paso 1: Separa la parte entera (1) de la decimal (0.75). Paso 2: Convierte 0.75 a fracción: 75/100. Paso 3: Simplifica: 75/100 = 3/4. Paso 4: El número mixto es 1 3/4.
¿Por qué 0.125 = 1/8?
+0.125 tiene tres cifras decimales, así que inicialmente es 125/1000. Para simplificar, divide ambos por su máximo común divisor (125): 125÷125 = 1 y 1000÷125 = 8, resultando en 1/8.
¿Qué errores comunes se cometen al convertir decimales a fracciones?
+Los errores más frecuentes son: usar el denominador incorrecto (no contar bien las cifras decimales), olvidar simplificar la fracción resultante, y confundir la posición del numerador y denominador al escribir la fracción final.
¿Cómo verificar si la conversión de decimal a fracción es correcta?
+Divide el numerador entre el denominador de tu fracción resultante. Si obtienes el decimal original, la conversión es correcta. Por ejemplo: para verificar que 0.4 = 2/5, calcula 2÷5 = 0.4 ✓