Domina la conversión de números decimales a fracciones simples con ejercicios paso a paso. Aprende a identificar décimas, centésimas y milésimas fácilmente.
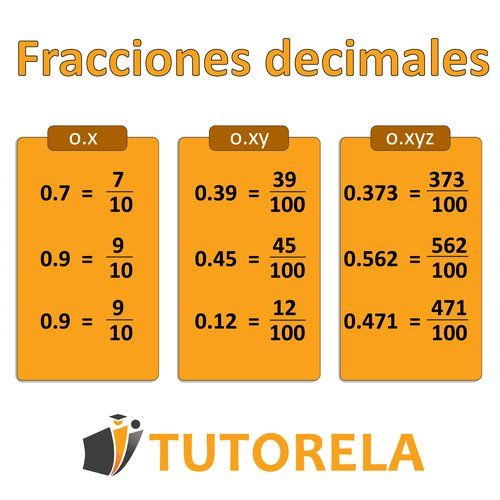
Para convertir un número decimal a fracción simple
nos preguntaremos cómo se lee el número decimal
Si utilizamos la palabra décimas, colocaremos en el denominador
Si utilizamos la palabra centésimas, colocaremos en el denominador
Si utilizamos la palabra milésimas, colocaremos en el denominador.
El número en sí lo colocaremos en el numerador.
*Si la cifra de los enteros difiere de , la anotaremos al lado de la fracción simple.
Elija la fracción decimal adecuada:
\( \frac{61}{100}= \)
Elija la fracción decimal adecuada:
Escribe la fracción simple en forma decimal
Como la fracción es divisible por 10, movemos el punto decimal un lugar a la izquierda y obtenemos:
Agreguemos el cero a la izquierda del punto decimal y obtenemos:
Respuesta:
0.7
Elija la fracción decimal adecuada:
Escribe la fracción simple en forma decimal
Como la fracción está dividida por 10, movemos el punto decimal un lugar a la izquierda y obtenemos:
Agregamos el cero a la izquierda del punto decimal y obtenemos:
Respuesta:
0.5
Prestemos atención a dónde está ubicado el punto decimal en el número.
Recuerda:
Un número después del punto decimal representa décimas
Dos números después del punto decimal representan centésimas
Tres números después del punto decimal representan milésimas
Y así sucesivamente
En este caso hay tres números después del punto decimal, por lo que el número se divide entre 1000
Escribe la fracción de la siguiente manera:
Eliminamos los ceros extra y obtenemos:
Respuesta:
Elija la fracción decimal adecuada:
Respuesta:
0.01
Elija la fracción decimal adecuada:
Respuesta:
0.2