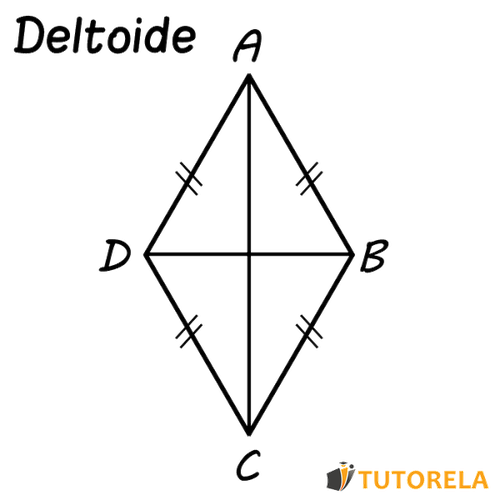
Deltoide para noveno grado - Ejemplos, Ejercicios y Soluciones

El deltoide y todo lo que necesitas saber para comprobarlo

¿Qué es un deltoide o cometa?

En geometría, un deltoide se define como un cuadrilátero que consta de $2$ triángulos isósceles que están en una sola base.

Entonces, ¿cuál es la identificación de deltoide en la familia de los cuadriláteros?

Un cuadrilátero que tiene 2 pares de lados adyacentes iguales

Ejemplo:

Si se proporciona : $AD=AB,DC=BC$

Entonces: $ABCD$ es un deltoide por definición.

2 triángulos isósceles con una base común que forman un deltoide.
La suma de los ángulos en el deltoide es $360°$ grados.
Área del deltoide contiene el número de cuadriláteros que cubren las partes de la llanura seleccionada.
El perímetro del deltoide Es la longitud del hilo con el que bordeamos el contorno del deltoide y se mide en unidades de longitud de metros o cm.

Practicar Deltoide para noveno grado

Ejercicio 1

Dado el deltoide de la figura:

¿Cuál es el área?

Ejercicio 2

Dado el deltoide ABCD

La diagonal AC=8 es el área del deltoide es 32 cm²

Calcula la diagonal DB

Ejercicio 3

Dado ABCD deltoide AB=BC DC=AD

Las diagonales del deltoide se cortan en el punto 0

Dado BD=14 El área del deloide es 42 cm²

Calcula el lado AO

Ejercicio 4

Dado el deltoide ABCD

diagonal DB=10

CB=4

¿Es posible calcular el área del deltoide? Si es así, ¿cuál es?

Ejercicio 5

Dado el deltoide ABCD

Halla el área

ejemplos con soluciones para Deltoide para noveno grado

Ejercicio #1

Dado el deltoide de la figura:

¿Cuál es el área?

Solución en video

Solución Paso a Paso

En un principio, recordemos la fórmula del área de un deltoide

$\frac{Diagonal1\times Diagonal2}{2}$

Ambos datos ya existen, por lo que podemos colocarlos en la fórmula:

(4*7)/2

28/2

Respuesta

Ejercicio #2

Dado el deltoide ABCD

La diagonal AC=8 es el área del deltoide es 32 cm²

Calcula la diagonal DB

Solución en video

Solución Paso a Paso

Primero, recordamos la fórmula del área del deltoide: multiplicar las longitudes de las diagonales entre sí y dividir este producto por 2.

Reemplazamos los datos sabidos en la fórmula:

$\frac{8\cdot DB}{2}=32$

Simplificamos el 8 y el 2:

$4DB=32$

Dividimos por 4

$DB=8$

Respuesta

8 cm

Ejercicio #3

Dado ABCD deltoide AB=BC DC=AD

Las diagonales del deltoide se cortan en el punto 0

Dado BD=14 El área del deloide es 42 cm²

Calcula el lado AO

Solución en video

Solución Paso a Paso

Reemplazamos los datos que tenemos en la fórmula del área del deltoide:

Diagonal por diagonal dividida por 2, reemplazamos los datos existentes en la fórmula:

$S=\frac{AC\times BD}{2}$

$42=\frac{AC\times14}{2}$

Multiplicamos por 2 para deshacernos del denominador:

$14AC=84$

Dividimos por 14:

$AC=6$

Prestemos atención que nos preguntaron sobre AO.

Se sabe que en un rombo, la diagonal principal cruza a la segunda diagonal, por lo tanto:

$AO=\frac{AC}{2}=\frac{6}{2}=3$

Respuesta

3 cm

Ejercicio #4

Dado el deltoide ABCD

diagonal DB=10

CB=4

¿Es posible calcular el área del deltoide? Si es así, ¿cuál es?

Solución en video

Respuesta

No se puede

Ejercicio #5

Dado el deltoide ABCD

Halla el área

Solución en video

Respuesta

$12$ cm²

Ejercicio 1

Dado el deltoide ABCD

Halla el área

Ejercicio 2

Dado el deltoide ABCD

Halla el área

Ejercicio 3

Dado el deltoide ABCD

Halla el área

Ejercicio 4

Dado el deltoide ABCD

Halla el área

Ejercicio 5

Respuesta

$20$ cm²

Ejercicio 1

Dado el deltoide ABCD

Halla el área

Ejercicio 2

Dado el deltoide ABCD

Halla el área

Ejercicio 3

Dado el deltoide ABCD

Halla el área

Ejercicio 4

Dado el deltoide ABCD

Halla el área

Ejercicio 5

Respuesta

Deltoide convexo