Identificación de un triángulo isósceles

Cuando tengamos un triángulo, podremos identificar que se trata de uno isósceles si se cumple, por lo menos, una de las siguientes condiciones:

1) Si el triángulo tiene dos ángulos iguales - El triángulo es isósceles.
2) Si en el triángulo la altura también corta el ángulo del vértice - El triángulo es isósceles.
3) Si en el triángulo la altura también es la mediana - El triángulo es isósceles.
4) Si en el triángulo la mediana también es la bisectriz - El triángulo es isósceles.

Antes de que hablemos acerca de cómo identificar un triángulo isósceles recordaremos que se trata de un triángulo con dos lados (o aristas) de la misma longitud - Esto significa que los ángulos de la base también son iguales.
Además, en un triángulo isósceles, la mediana de la base, la bisectriz y la altura son lo mismo, es decir, coinciden.
Veámoslo ilustrado:

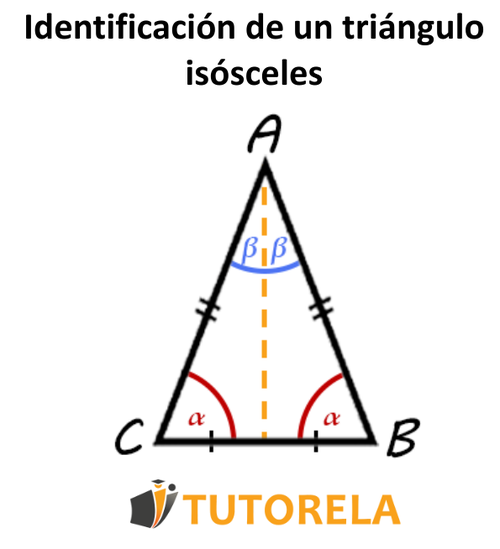
Estas magníficas propiedades del triángulo isósceles no pueden demostrarnos por sí mismas que se trate de un triángulo isósceles.
Entonces, ¿cómo se puede demostrar que nuestro triángulo es isósceles?

Si se cumple, por lo menos, una de las siguientes condiciones:
1) Si nuestro triángulo tiene dos ángulos iguales - El triángulo es isósceles.
Esto deriva de que los lados opuestos a ángulos iguales también son iguales, por lo tanto, si los ángulos son iguales, los lados también lo son.

2) Si en el triángulo la altura también corta el ángulo del vértice - El triángulo es isósceles.
3) Si en el triángulo la altura también es la mediana - El triángulo es isósceles.
4) Si en el triángulo la mediana también es la bisectriz - El triángulo es isósceles.
De hecho, podemos resumir las pautas $2$ y $4$ y escribir una sola condición:
Si dos de éstos coinciden - la mediana, la altura y la bisectriz - El triángulo es isósceles.

Genial, ahora ya sabes identificar triángulos isósceles con facilidad y rapidez.

Si está interesado en aprender más sobre otros temas de ángulos, puede ingresar a uno de los siguientes artículos:

• Suma de los ángulos internos de un polígono
• Ángulos en hexágonos y octágonos regulares
• Medida de un ángulo de un polígono regular
• Suma de los ángulos externos de un polígono
• Ángulo exterior de un triángulo
• Relaciones entre ángulos y lados del triángulo
• La relación entre las longitudes de los lados de un triángulo

En el blog de Tutorela encontrarás una variedad de artículos sobre matemáticas.