Preguntas Frecuentes
Todo lo que necesitas saber Segmento medio de un trapecio
¿Qué es el segmento medio de un trapecio y cuáles son sus propiedades?
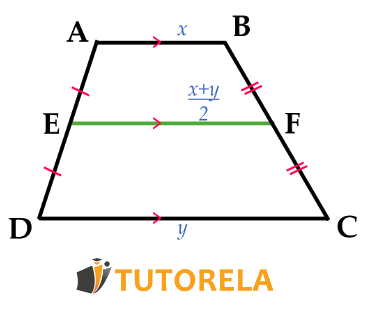
+ El segmento medio de un trapecio es la recta que une los puntos medios de los lados no paralelos. Sus propiedades principales son: 1) Es paralelo a ambas bases, 2) Su longitud es el promedio de las bases: EF = (AB + DC)/2, 3) Divide los lados laterales por la mitad.
¿Cómo se calcula la longitud del segmento medio de un trapecio?
+ La longitud del segmento medio se calcula con la fórmula: EF = (AB + DC)/2, donde AB y DC son las longitudes de las bases del trapecio. Es decir, el segmento medio mide la mitad de la suma de las bases.
¿Cuáles son las condiciones para demostrar que existe un segmento medio?
+ Hay dos condiciones principales: 1) Si una recta une los puntos medios de ambos lados no paralelos, entonces es el segmento medio. 2) Si una recta parte del punto medio de un lado y es paralela a una base, entonces es el segmento medio y corta el otro lado por la mitad.
¿Por qué el segmento medio es paralelo a las bases del trapecio?
+ El segmento medio es paralelo a las bases porque conecta los puntos medios de los lados no paralelos del trapecio. Esta propiedad se deriva del teorema del segmento medio y es una característica fundamental que siempre se cumple.
¿Cómo resolver ejercicios donde se pide demostrar que BF = FC?
+ Para demostrar que BF = FC, debes verificar que: 1) La recta EF parte del punto medio del otro lado (AE = DE), 2) EF es paralela a una de las bases (AB∥EF). Si se cumplen estas condiciones, entonces EF es el segmento medio y divide el segundo lado por la mitad.
¿Qué diferencia hay entre el segmento medio de un triángulo y un trapecio?
+ En un triángulo, el segmento medio une los puntos medios de dos lados y es paralelo al tercer lado con longitud igual a la mitad. En un trapecio, une los puntos medios de los lados no paralelos y su longitud es el promedio de las dos bases.
¿Cuáles son los errores más comunes al resolver problemas del segmento medio?
+ Los errores más frecuentes son: 1) Confundir la fórmula con la del triángulo, 2) No verificar que la recta sea paralela a las bases, 3) No comprobar que los puntos sean efectivamente los puntos medios, 4) Aplicar incorrectamente la fórmula EF = (AB + DC)/2.
¿En qué situaciones prácticas se aplica el segmento medio del trapecio?
+ Se aplica en arquitectura para calcular vigas de soporte, en ingeniería civil para diseñar estructuras trapezoidales, en carpintería para cortes precisos, y en problemas de geometría analítica para encontrar puntos medios en figuras complejas.