El segmento medio de un triángulo tiene tres propiedades principales:
- El segmento medio cruza exactamente por el medio a los dos lados que lo determinan.
- El segmento medio es paralelo al tercer lado del triángulo.
- El segmento medio mide la mitad de la longitud del lado dispuesto paralelamente a él.
Veamos las propiedades del segmento medio de un triángulo en la siguiente ilustración:
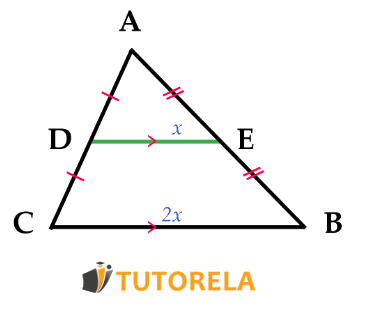
Si
entonces