El segmento medio es un segmento que conecta los puntos medios de 2 lados.
Segmento medio
Segmento medio de un triángulo
¡Pruébate en segmento medio!
Dado un trapecio isósceles, ¿el segmento punteado es un segmento medio del trapecio?
Demostración del segmento medio de un triángulo
Podremos demostrar que hay un segmento medio en un triángulo si se cumple, al menos, alguna de las siguientes condiciones:
- Si en un triángulo hay una línea recta que se extiende desde la mitad de un lado hasta la mitad de otro lado, podemos determinar que se trata de un segmento medio y, por lo tanto, que mide la mitad de la longitud del tercer lado, al cual, de hecho, también es paralela.
- Si una línea recta corta a uno de los lados de un triángulo y ésta es paralela a otro lado del triángulo, significa que se trata de un segmento medio y que, por lo tanto, también corta al tercer lado del triángulo y mide la mitad del largo del lado que es paralelo a ella.
- Si en un triángulo hay un segmento cuyos extremos se encuentran en dos de sus lados, mide la mitad de la longitud del tercer lado y le es paralelo, podemos determinar que dicho segmento es un segmento medio y, por lo tanto, corta a los lados que toca justo por el medio.
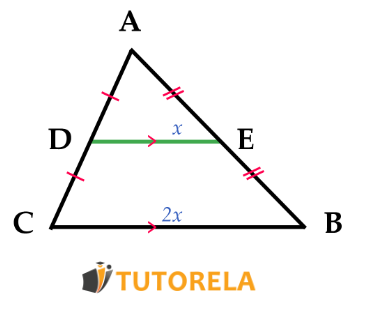
Segmento medio de un trapecio
El segmento medio de un trapecio divide en dos partes iguales los dos lados de los que sale y, además, es paralelo a ambas bases del trapecio y mide la mitad del largo de éstas.
Dado un trapecio isósceles, ¿el segmento punteado es un segmento medio del trapecio?
Dado el trapecio isósceles, EF es paralela a la base del trapecio
¿El segmento EF es la sección media en el trapecio?
Dado que DE es una sección media en el triángulo ABC, ¿cuál es la longitud del lado DE?
Demostración del segmento medio de un trapecio
Podremos demostrar que hay un segmento medio en un trapecio si se cumple, al menos, una de las siguientes condiciones:
- Si en un trapecio hay una línea recta que se extiende desde la mitad de un lado hasta la mitad de otro lado, podemos determinar que se trata de un segmento medio y, por lo tanto, es paralelo a ambas bases del trapecio y mide la mitad del largo de éstas.
- Si en un trapecio hay una línea recta que sale de un lado y es paralela a una de las bases del trapecio, podemos determinar que se trata de un segmento medio y, por lo tanto, es paralelo a ambas bases del trapecio, mide la mitad del largo de éstas dos y también corta por el medio al segundo lado que toca.
Segmento medio
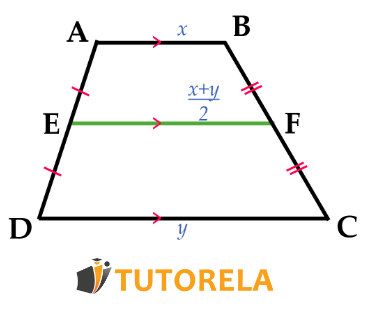
El segmento medio es un segmento que conecta los puntos medios de 2 lados.
Es muy simple recordar el significado de este término ya que la palabra «medio» ya nos dice que se trata del punto medio, entonces, cuando nos topemos con el concepto «segmento medio» recordaremos que éste une los puntos medios de dos lados.
Estamos aquí para enseñarte todo lo que debes saber acerca del segmento medio, desde la demostración hasta las magníficas propiedades del segmento que nos ayudarán a resolver ejercicios.
En primer lugar hablaremos del segmento medio de un triángulo y luego pasaremos al segmento medio de un trapecio.
Dado que DE es la sección media en el triángulo ABC, ¿cuál es la longitud del lado DE?
Dado que DE es la sección media en el triángulo ABC, ¿cuál es la longitud del lado DE?
Dado que DE es una sección media en el triángulo ABC, ¿cuál es la longitud del lado DE?
Segmento medio de un triángulo
El segmento medio de un triángulo cruza por el medio a los dos lados de los cuales sale, pero, más allá de esto, cuenta con dos magníficas propiedades que podremos utilizar luego de demostrar que dicho segmento es, de hecho, un segmento medio del triángulo.
Propiedades del segmento medio de un triángulo
El segmento medio de un triángulo mide la mitad del largo del tercer lado
y también le es paralelo.
Veámoslo en una ilustración
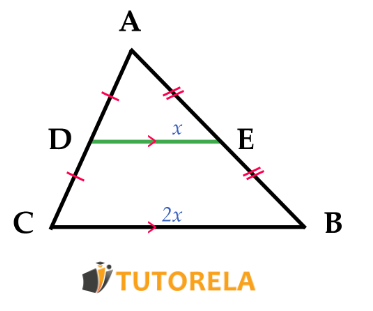
Si
entonces
Dado que DE es una sección media en el triángulo ABC, ¿cuál es la longitud del lado DE?
Dado que DE es una sección media en el triángulo ABC, ¿cuál es la longitud del lado DE?
Dado que DE es la sección media en el triángulo ABC, ¿cuál es la longitud del lado DE?
¿Cómo demostraremos que hay un segmento medio en el triángulo?
El teorema habla de las propiedades del segmento medio y de su definición.
Podremos determinar que tenemos ante nosotros un segmento medio de un triángulo si se cumple, al menos, una de las siguientes condiciones:
- Si en un triángulo hay una línea recta que se extiende desde la mitad de un lado hasta la mitad de otro lado, podemos determinar que se trata de un segmento medio y, por lo tanto, que mide la mitad de la longitud del tercer lado, al cual, de hecho, también es paralela.
Es decir, si sabemos que:
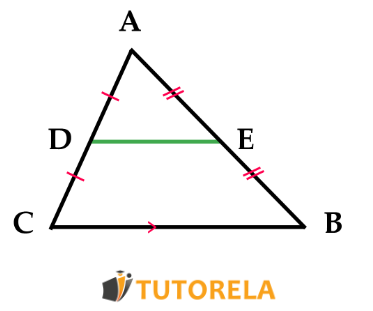
Entonces, podremos determinar que:
se trata de un segmento medio de un triángulo y, por consiguiente,
- Si una línea recta corta a uno de los lados de un triángulo y ésta es paralela a otro lado del triángulo, significa que se trata de un segmento medio y que, por lo tanto, también corta al tercer lado del triángulo y mide la mitad del largo del lado que es paralelo a ella.
Es decir, si sabemos que:
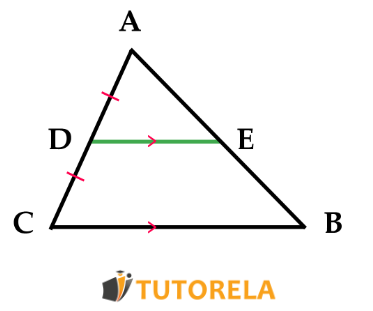
y también
Entonces, podremos determinar que:
se trata de un segmento medio de un triángulo y, por consiguiente,
y también
- Si en un triángulo hay un segmento cuyos extremos se encuentran en dos de sus lados, mide la mitad de la longitud del tercer lado y le es paralelo, podemos determinar que dicho segmento es un segmento medio y, por lo tanto, corta a los lados que toca justo por el medio.
Es decir, si sabemos que:
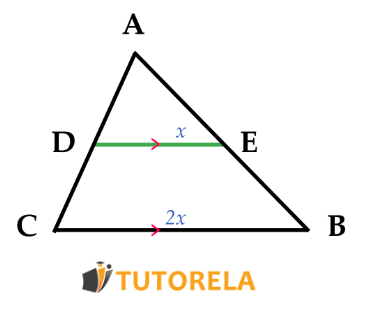
y también
Entonces, podremos determinar que:
se trata de un segmento medio de un triángulo y, por consiguiente,
y también
Algunas acotaciones para una victoria asegurada
- Nos percatamos de que es fácil recordar que el segmento medio es un segmento que sale del punto medio de un lado hacia el punto medio de otro lado ya que la palabra misma nos lo revela. Pero ¡presta atención! No en todos los casos se usará el concepto «segmento medio», a veces se dirá mediana para describir la línea que corta un lado por el punto medio.
Por lo tanto, cuando te encuentres con la palabra «mediana» recuerda que probablemente debas buscar un segmento medio del triángulo. - Hay figuras con medianas por definición. Por ejemplo, las diagonales del paralelogramo se intersecan por el medio, o sea, son medianas, por lo tanto, si sacamos del punto de intersección de las diagonales un segmento que vaya hasta la arista del paralelogramo, éste será un segmento medio en el correspondiente triángulo que se ha formado por la diagonal.
Segmento medio de un trapecio
El segmento medio de un trapecio es muy similar en sus propiedades al segmento medio de un triángulo... Es lógico ya que, de todas maneras, aún estamos hablando del segmento medio.
Dado que DE es la sección media en el triángulo ABC, ¿cuál es la longitud del lado DE?
Dado que DE es la sección media en el triángulo ABC, ¿cuál es la longitud del lado DE?
Dado que DE es una sección media en el triángulo ABC, ¿cuál es la longitud del lado DE?
Propiedades del segmento medio de un trapecio:
El segmento medio de un trapecio divide en dos partes iguales los dos lados de los que sale y, además, es paralelo a ambas bases del trapecio y mide la mitad del largo de éstas.
Observa, como ya hemos mencionado, sus propiedades son similares a las del segmento medio del triángulo.
Las dos expresiones que debes recordar son: paralelo y mide la mitad.
Pero, no te confundas, en el trapecio el segmento medio mide la mitad de la longitud de las bases - es decir, la mitad del largo de las dos bases juntas.
Podrás utilizar estas propiedades luego de demostrar que hay un segmento medio en el trapecio.
Veamos las propiedades del segmento medio en una ilustración:
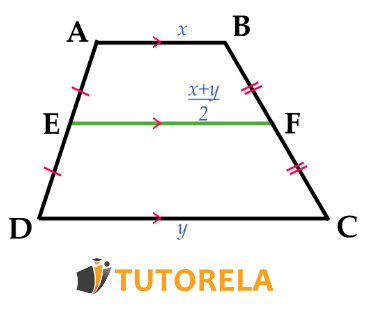
Si Segmento medio
entonces:
¿Cómo podemos demostrar un segmento medio en un trapecio?
El teorema del segmento medio en un trapecio trata de las propiedades.
Si se cumple, al menos, una de las siguientes condiciones podremos determinar que se trata de un segmento medio en un trapecio:
- Si en un trapecio hay una línea recta que se extiende desde la mitad de un lado hasta la mitad de otro lado, podemos determinar que se trata de un segmento medio y, por lo tanto, es paralelo a ambas bases del trapecio y mide la mitad del largo de éstas.
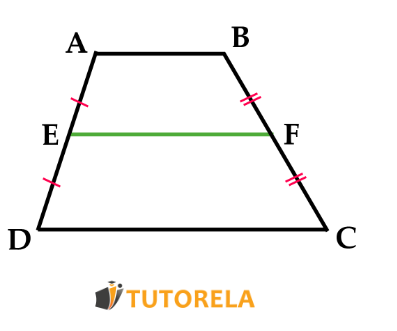
Es decir, si sabemos que:
y también
Entonces, podremos determinar que:
es un segmento medio del trapecio
Entonces:
Si en un trapecio hay una línea recta que sale de un lado y es paralela a una de las bases del trapecio, podemos determinar que se trata de un segmento medio y, por lo tanto, es paralelo a ambas bases del trapecio, mide la mitad del largo de éstas dos y también corta por el medio al segundo lado que toca.
Es decir, si sabemos que:
y también
Entonces, podremos determinar que:
es un segmento medio del trapecio y, por consiguiente:
Si te interesa este artículo también te pueden interesar los siguientes artículos:
- Segmento medio de un triángulo
- Segmento medio de un trapecio
- Suma de los ángulos internos de un polígono
- Ángulos en hexágonos y octágonos regulares
- Medida de un ángulo de un polígono regular
- Suma de los ángulos externos de un polígono
- Relaciones entre ángulos y lados del triángulo
- La relación entre las longitudes de los lados de un triángulo
- Identificación de un triángulo isósceles
- ¿Cómo se calcula el área de un trapecio?
- Simetría en trapecios
- Diagonales de un trapecio isósceles
- ¿Cómo se calcula el perímetro de un trapecio?
- Características y tipos de trapecios
En el blog de Tutorela encontrarás una variedad de artículos sobre matemáticas.
Ejemplos y ejercicios con soluciones del segmento medio
Ejercicio #1
Dado un trapecio isósceles, ¿el segmento punteado es un segmento medio del trapecio?
Solución en video
Respuesta
No verdadero
Ejercicio #2
Dado un trapecio isósceles, ¿el segmento punteado es un segmento medio del trapecio?
Solución en video
Respuesta
No verdadero
Ejercicio #3
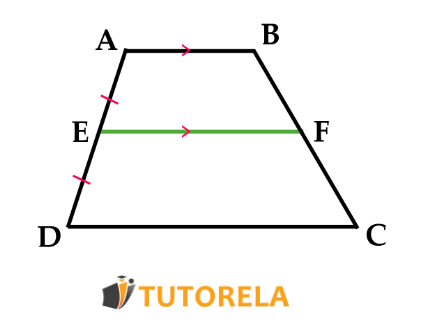
Dado el trapecio isósceles, EF es paralela a la base del trapecio
¿El segmento EF es la sección media en el trapecio?
Solución en video
Respuesta
Verdadero
Ejercicio #4
Dado que DE es una sección media en el triángulo ABC, ¿cuál es la longitud del lado DE?
Solución en video
Respuesta
11
Ejercicio #5
Dado que DE es la sección media en el triángulo ABC, ¿cuál es la longitud del lado DE?
Solución en video
Respuesta
12
Dado que DE es la sección media en el triángulo ABC, ¿cuál es la longitud del lado DE?
Dado que DE es la sección media en el triángulo ABC, ¿cuál es la longitud del lado DE?
Dado un trapecio isósceles, ¿el segmento punteado es un segmento medio del trapecio?
- Altura del triángulo
- Suma de los ángulos internos de un triángulo
- Los lados o aristas de un triángulo
- Trapecios
- Simetría en trapecios
- Diagonales de un trapecio isósceles
- Área de un trapecio
- Perímetro de un trapecio
- Trapecio isósceles
- Ángulo exterior de un triángulo
- Relaciones entre ángulos y lados del triángulo
- La relación entre las longitudes de los lados de un triángulo
- Segmento medio
- Segmento medio de un triángulo
- Segmento medio de un trapecio
- Área
- Perímetro
- Triángulo
- Tipos de triángulos
- Triángulo obtuso
- Triángulo equilátero
- Identificación de un triángulo isósceles
- Triángulo escaleno
- Triángulo agudo
- Triángulo isósceles
- Área de un triángulo
- Área de un triángulo rectángulo
- Área del triángulo isósceles
- Área del triángulo escaleno
- Área del triángulo equilátero
- Perímetro de un triángulo
- Áreas de Polígonos para 7º Grado
- Triángulo Rectángulo
- Área de un trapecio rectángulo
- Área de un trapecio isósceles
- Mediana en un triángulo
- Centro de un Triángulo - El Centroide - El Punto de Intersección de las Medianas
- ¿Cómo calculamos el área de figuras complejas?
- ¿Cómo calculamos el perímetro de los polígonos?
- Todos los términos en el cálculo de triángulos
- ¿Cómo calcular el área de un triángulo usando trigonometría?
- Orden de operaciones básicas: suma, resta, multiplicación y división
- Orden de las operaciones básicas (potencias)
- Orden de operaciones básicas: raíces
- El 0 y el 1 en el orden de las operaciones
- Inverso multiplicativo
- Orden de las operaciones: paréntesis
- La propiedad conmutativa
- La propiedad asociativa
- Cómo calcular el área de un ortoedro
- Potenciación de números enteros
- Las Tablas de Multiplicar
- Fracciones









