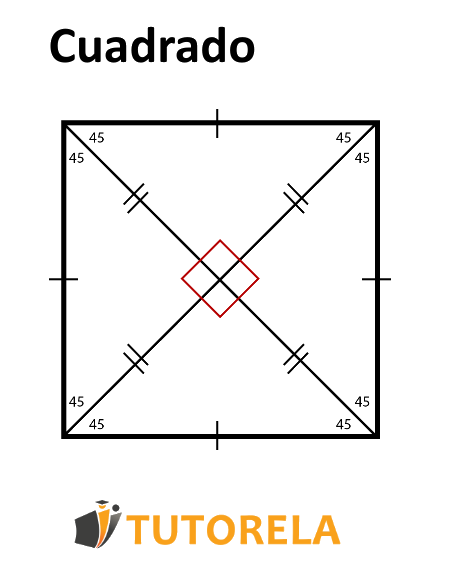
Un cuadrilátero cuyos lados (o aristas) son todos iguales y todos sus ángulos también lo son, es un cuadrado.
Además, un cuadrado es una combinación entre un paralelogramo, un rombo y un rectángulo.
Por lo tanto, el cuadrado cuenta con todas las propiedades del paralelogramo, del rombo y del rectángulo.