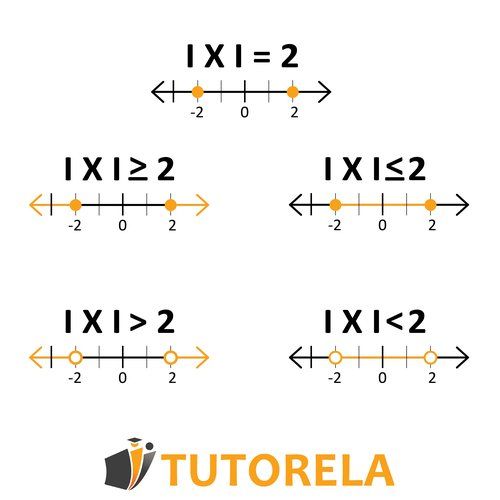
Cuando te encuentres con signos como o , Sabrás que es desigualdad.
El resultado de la desigualdad será un cierto rango de valores que tendrás que encontrar.
Una regla importante a tener en cuenta: cuando duplicas o divides los dos lados de la operación, el signo de la desigualdad se invierte!
Podemos resolver desigualdades con valor absoluto de formas:
En el método geométrico y en el método algebraico.
Dado:
\( \left|x+2\right|<3 \)
¿Cuál de las siguientes afirmaciones es necesariamente cierta?
Dado:
\( \left|x-4\right|<8 \)
¿Cuál de las siguientes afirmaciones es necesariamente cierta?
Dado:
\( \left|x+4\right|>13 \)
¿Cuál de las siguientes afirmaciones es necesariamente cierta?
Dado:
\( \left|x-5\right|>11 \)
¿Cuál de las siguientes afirmaciones es necesariamente cierta?
Dado:
\( \left|x-5\right|>-11 \)
¿Cuál de las siguientes afirmaciones es necesariamente cierta?
Dado:
\left|x+2\right|<3
¿Cuál de las siguientes afirmaciones es necesariamente cierta?
-5 < x < 1
Dado:
\left|x-4\right|<8
¿Cuál de las siguientes afirmaciones es necesariamente cierta?
-4 < x < 12
Dado:
\left|x+4\right|>13
¿Cuál de las siguientes afirmaciones es necesariamente cierta?
x>9 o x<-17
Dado:
\left|x-5\right|>11
¿Cuál de las siguientes afirmaciones es necesariamente cierta?
x>16 o x<-6
Dado:
\left|x-5\right|>-11
¿Cuál de las siguientes afirmaciones es necesariamente cierta?
Para cualquier x
Dado:
\( \left|2x-4\right|<8 \)
¿Cuál de las siguientes afirmaciones es necesariamente cierta?
Dado:
\( \left|3x+9\right|<18 \)
¿Cuál de las siguientes afirmaciones es necesariamente cierta?
Dado:
\( \left|5x-10\right|>15 \)
¿Cuál de las siguientes afirmaciones es necesariamente cierta?
Dado:
\( \left|4x+12\right|>16 \)
¿Cuál de las siguientes afirmaciones es necesariamente cierta?
Dado:
\( \left|2x-1\right|>-10 \)
¿Cuál de las siguientes afirmaciones es necesariamente cierta?
Dado:
\left|2x-4\right|<8
¿Cuál de las siguientes afirmaciones es necesariamente cierta?
-2 < x < 6
Dado:
\left|3x+9\right|<18
¿Cuál de las siguientes afirmaciones es necesariamente cierta?
-9 < x < 3
Dado:
\left|5x-10\right|>15
¿Cuál de las siguientes afirmaciones es necesariamente cierta?
x>5 o x<-1
Dado:
\left|4x+12\right|>16
¿Cuál de las siguientes afirmaciones es necesariamente cierta?
x>1 o x<-7
Dado:
\left|2x-1\right|>-10
¿Cuál de las siguientes afirmaciones es necesariamente cierta?
Para toda x
Dado:
\( ||1-4|+3|-|a|<0 \)
¿Cuál de las siguientes afirmaciones es necesariamente cierta?
Dado:
\( |a|-|18-9|+|4|<0 \)
¿Cuál de las siguientes afirmaciones es necesariamente cierta?
Dado:
\( \Vert-4+8|-2|-|a|>0 \)
Dado:
\( |a|-||5-4|-1|>0 \)
Dado:
\( |a|+||5-1|+3-4|<0 \)
¿Cuál de las siguientes afirmaciones es necesariamente cierta?
Dado:
||1-4|+3|-|a|<0
¿Cuál de las siguientes afirmaciones es necesariamente cierta?
a<-6
Dado:
|a|-|18-9|+|4|<0
¿Cuál de las siguientes afirmaciones es necesariamente cierta?
-13 < a < 13
Dado:
\Vert-4+8|-2|-|a|>0
2>a>-2
Dado:
|a|-||5-4|-1|>0
Para cualquier valor de a
Dado:
|a|+||5-1|+3-4|<0
¿Cuál de las siguientes afirmaciones es necesariamente cierta?
Para cualquier valor de a