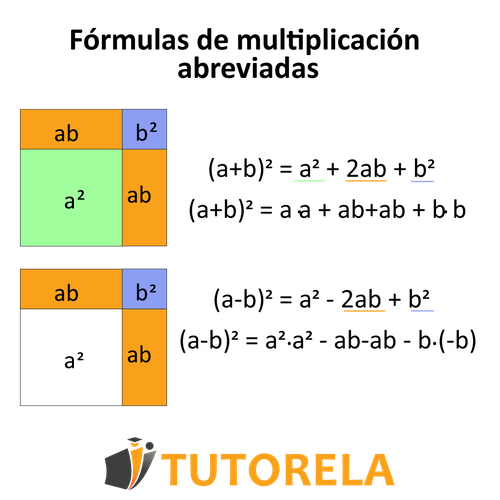
Esta fórmula es una de las fórmulas abreviadas y nos describe la suma cuadrada de dos números.
Es decir, cuando nos encontramos con dos números con un signo más (suma) y están entre paréntesis y se elevan como una expresión al cuadrado, podemos usar esta fórmula.
Presta atención - La fórmula funciona también expresiones no algebraicas o combinaciones combinadas con números e incógnitas.
Es bueno sabe que es muy similar a la fórmula para la resta de cuadrados y difiere solo en el signo menos del elemento central.