Las rectas paralelas son rectas que pertenecen al mismo plano (son coplanares) y nunca se encuentran (no se cortan).
Sean dos rectas paralelas y como las que se muestran a continuación.
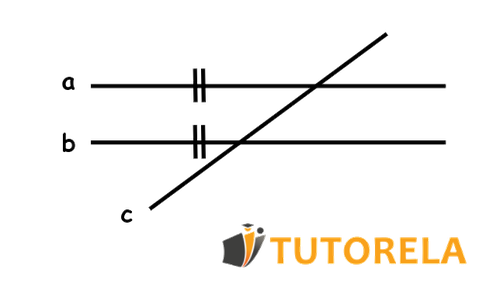
Si afirmamos lo siguiente:
La recta es paralela a la recta
podemos decir lo mismo usando el lenguaje matemático del siguiente modo:
¿Qué tienen en común las 4 figuras?
¿Cuáles rectas son perpendiculares entre sí?
Recordemos que las rectas perpendiculares son rectas que forman entre sí un ángulo recto de 90 grados.
El único dibujo donde se puede ver que las rectas forman un ángulo recto de 90 entre sí es el dibujo A.
Respuesta:
¿Qué rectas son perpendiculares entre sí?
Las rectas perpendiculares son rectas que forman entre sí un ángulo recto de 90 grados.
El único dibujo donde las rectas forman un ángulo recto de 90 grados entre sí es el dibujo A.
Respuesta:
¿En cuáles de las figuras hay rectas paralelas?
Las rectas paralelas son rectas, si las continuamos nunca se encontrarán.
En los dibujos A+B+D si continuamos las rectas veremos que en un punto determinado se juntan.
En el dibujo C, las rectas nunca se encontrarán, por lo tanto son líneas paralelas.
Respuesta:
Las rectas no son del mismo tamaño, ¿son paralelas?
Recuerda las propiedades de las rectas paralelas.
Como no existe conexión entre el tamaño de la recta y el paralelismo, las líneas son realmente paralelas.
Respuesta:
Verdadero
¿Qué podemos decir de las siguientes rectas?
Recordemos las diferentes propiedades de las rectas.
Las rectas no son paralelas ya que se encuentran.
Las rectas no son perpendiculares ya que no forman un ángulo recto de 90 grados entre sí.
Por lo tanto, ninguna respuesta es correcta.
Respuesta:
Ninguna respuesta es correcta