$$ a $$ es paralela a $$ b $$ Determina cuál de las afirmaciones es correcta. α α α β β β γ γ γ δ δ δ a a a b b b

$$ \beta,\gamma $$ Colaterales $$ \alpha,\delta $$ Alternos

$$ \alpha,\beta $$ Colaterales $$ \gamma,\delta $$ Adyacentes

$$ \alpha,\beta $$ Adyacentes $$ \gamma,\delta $$ Alternos

¿Qué ángulos están marcados con la letra A en el dibujo? ¿Y cuáles con la letra B? Responda la pregunta asumiendo que ABCD es un rectángulo A A A B B B C C C D D D B B A A

A- correspondientes B- adyacentes

A- correspondientes B- colaterales

A- opuestos por el vértice B- opuestos por el vértice

Dado el rombo de la figura, ¿Cuáles son los ángulos marcados? B A A B

A- correspondientes B- alternos

A- correspondientes B- opuestos por el vértice

A- opuestos por el vértice B- alternos

A- colaterales B- correspondientes

Dado el paralelogramo del dibujo, calcula los ángulos marcados 30 20 <path d="m271.87 455.39-.28.35q-1.33 0-1.33-.7 0-1.96 2.38-5.6 4.9-7.07 11.27-7.21 6.3 0 9.31 7.7 2.59 6.51 2.87 14.28 5.53-13.86 9.24-20.72.21-.49.84-.49.84 0 .84.7 0 .35-1.33 2.66-5.18 10.29-9.03 21.35-.28.84-.49 1.54-.28.91-.56 2.73-.63 4.9-2.59 12.04-1.19 3.99-2.24 4.2-.91 0-.91-1.26 0-2.87 3.5-14.7.07-.14.14-.35.84-2.38.84-6.86 0-16.45-9.8-17.71-.77-.07-1.54-.07-4.97 0-8.33 3.43l-.07.07q-1.82 1.89-2.73 4.62Z" paint-order="stroke fill markers"> β α

$$ \alpha=30 $$ $$ \beta=150 $$ $$ \gamma=20 $$

$$ \alpha=150 $$ $$ \beta=30 $$ $$ \gamma=20 $$

$$ \alpha=30 $$ $$ \beta=150 $$ $$ \gamma=30 $$

$$ \alpha=30 $$ $$ \beta=30 $$ $$ \gamma=20 $$

Dado a paralelo a b Halla los ángulos del dibujo 115 115 115 1 1 1 2 2 2 3 3 3 4 4 4 5 5 5 6 6 6 7 7 7 a a a b b b

1,3= 65 ° 2,4,6= 115 ° 5,7= 75 °

Ejercicios de Ángulos Adyacentes - Problemas y Práctica

Practica con ejercicios de ángulos adyacentes en rectas paralelas. Aprende a calcular medidas, identificar tipos y resolver problemas paso a paso.

📚¿Qué vas a practicar con estos ejercicios?

Identificar ángulos adyacentes en intersecciones de rectas y distinguirlos de otros tipos
Aplicar la propiedad suplementaria: calcular ángulos que suman 180 grados
Resolver problemas con triángulos usando ángulos exteriores y adyacentes
Calcular medidas desconocidas en configuraciones de rectas paralelas y transversales
Distinguir entre ángulos adyacentes, correspondientes, alternos y opuestos por el vértice
Resolver ecuaciones algebraicas para encontrar valores de ángulos desconocidos

Entendiendo la Ángulos adyacentes

Explicación completa con ejemplos

¿Qué significa ángulo adyacente?

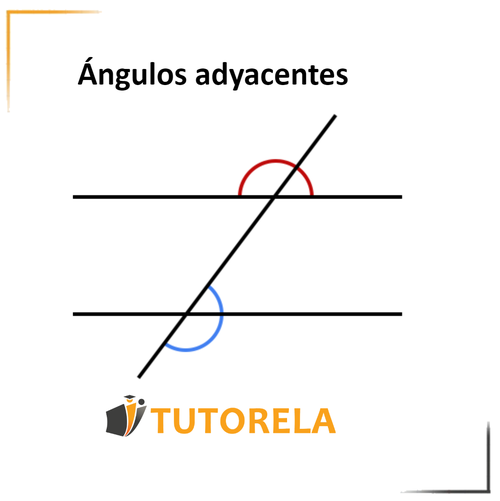
Los ángulos adyacentes son el par de ángulos que se forman cuando dos rectas que se cruzan entre sí. Estos ángulos se forman en el punto donde ocurre la intersección siendo uno adyacente al otro característica de la cual deriva su nombre. Otro par de ángulos que se forman en la intersección de dos rectas son los ángulos opuestos por el vértice, pero este par de ángulos son opuestos por el vértice y no adyacentes, por lo que no debemos confundirlos con los ángulos adyacentes. Los ángulos adyacentes siempre son suplementarios, es decir, juntos equivalen a $180°$ .

La siguiente ilustración muestra con dos ejemplos cómo son los ángulos adyacentes. Un ejemplo está pintado de rojo y el otro de azul.

Explicación completa

Practicar Ángulos adyacentes

Pon a prueba tus conocimientos con más de 48 cuestionarios

¿Cuáles ángulos en el dibujo son equiláteros?

Dado que a paralela a b

ejemplos con soluciones para Ángulos adyacentes

Soluciones paso a paso incluidas

Ejercicio #1

Las rectas en el dibujo son paralelas entre sí.

¿Qué ángulos se describen en la figura?

Solución Paso a Paso

Recordemos que los ángulos alternos se pueden definir como un par de ángulos que se pueden encontrar en el aspecto opuesto de una recta trazada para cortar dos líneas paralelas entre sí.

Además, estos ángulos se ubican en el nivel opuesto con respecto a la recta correspondiente a la que pertenecen.

Respuesta:

Alternos

Ejercicio #2

$a$ es paralela a

$b$

Determina cuál de las afirmaciones es correcta.

Solución Paso a Paso

Recuerda la definición de ángulos adyacentes:

Los ángulos adyacentes son ángulos cuya formación es posible en una situación en la que hay dos líneas rectas que se cruzan. Estos ángulos se forman en el punto donde se produce la intersección, uno contiguo al otro, y de aquí también sale su nombre.

Recuerda la definición de ángulos colaterales:

Dos ángulos formados cuando dos o más líneas paralelas son cortadas por una tercera línea. Los ángulos colaterales están del mismo lado de la línea de corte e incluso están a diferente altura en relación con la línea paralela a la que son adyacentes.

Por lo tanto, la respuesta C es correcta para esta definición.

Respuesta:

$\beta,\gamma$ Colaterales $\gamma,\delta$ Adyacentes

Solución en video

Ejercicio #3

¿En cuál de los dibujos hay ángulos $\alpha,\beta$ opuestos por el vértice?

Solución Paso a Paso

Recuerda la definición de ángulos opuestos por el vértice:

Los ángulos opuestos por el vértice son ángulos cuya formación es posible cuando dos rectas se cruzan, y se forman en el punto de intersección, una enfrentada a la otra. Los ángulos agudos son iguales en tamaño.

El dibujo de la respuesta A corresponde a esta definición.

Respuesta:

Solución en video

Ejercicio #4

¿Es posible tener dos ángulos adyacentes, uno de los cuales sea obtuso y el otro recto?

Solución Paso a Paso

Recuerda la definición de ángulos adyacentes:

Los ángulos adyacentes siempre se complementan hasta ciento ochenta grados, es decir, su suma es 180 grados.

Esta situación es imposible ya que un ángulo recto es igual a 90 grados, un ángulo obtuso es mayor a 90 grados.

Por lo tanto, en conjunto su suma será mayor que 180 grados.

Respuesta:

Falso

Solución en video

Ejercicio #5

¿Qué ángulos se describen en el dibujo?

Solución Paso a Paso

Como los ángulos no están en líneas paralelas, ninguna de las respuestas es correcta.

Respuesta:

Ninguna de las respuestas

Preguntas Frecuentes

Todo lo que necesitas saber Ángulos adyacentes

¿Cómo identificar si dos ángulos son adyacentes?

Los ángulos adyacentes se forman en la intersección de dos rectas, están uno al lado del otro (no opuestos) y siempre suman 180°. Si ves dos ángulos que comparten un vértice y un lado común, y juntos forman una línea recta, son adyacentes.

¿Cuál es la diferencia entre ángulos adyacentes y opuestos por el vértice?

Los ángulos adyacentes están uno al lado del otro y suman 180°, mientras que los opuestos por el vértice están enfrentados y son iguales. En una intersección de rectas, los adyacentes se complementan y los opuestos se igualan.

¿Cómo resolver problemas de ángulos adyacentes paso a paso?

1) Identifica que los ángulos son adyacentes, 2) Aplica que suman 180°, 3) Plantea la ecuación correspondiente, 4) Despeja la incógnita. Por ejemplo: si un ángulo mide 70°, el adyacente mide 180° - 70° = 110°.

¿Pueden dos ángulos obtusos ser adyacentes?

No, es imposible que dos ángulos obtusos (mayores a 90°) sean adyacentes. Como los ángulos adyacentes deben sumar exactamente 180°, y dos obtusos sumarían más de 180°, esta situación no puede ocurrir matemáticamente.

¿Qué tipos de ángulos se forman cuando una transversal corta rectas paralelas?

Se forman cuatro tipos principales: correspondientes (misma posición, iguales), alternos (lados opuestos, iguales), colaterales (mismo lado, suman 180°), y adyacentes (en cada intersección, suman 180°). Cada tipo tiene propiedades específicas para resolver problemas.

¿Cómo usar ángulos adyacentes para calcular ángulos de triángulos?

En triángulos con lados extendidos, el ángulo exterior y el interior del mismo vértice son adyacentes (suman 180°). Si conoces el exterior, restas de 180° para hallar el interior, luego usas que los tres interiores suman 180°.

¿Cuáles son los errores más comunes al trabajar con ángulos adyacentes?

Los errores principales son: confundirlos con opuestos por el vértice, olvidar que deben sumar 180°, no identificar correctamente cuáles ángulos son adyacentes en figuras complejas, y hacer errores algebraicos al plantear ecuaciones.

¿En qué situaciones de la vida real aplicamos los ángulos adyacentes?

Se aplican en arquitectura (esquinas de edificios), carpintería (uniones de maderas), navegación (cambios de rumbo), ingeniería civil (intersecciones de calles), y diseño gráfico (composiciones geométricas). Cualquier situación con intersecciones genera ángulos adyacentes.

Continúa tu viaje matemático

Domina primero la Ángulos adyacentes, luego avanza a estos temas relacionados que construyen sobre tus habilidades con fracciones

Temas sugeridos para practicar con anticipación

Líneas paralelas (Rectas paralelas)

Temas que se aprenden en secciones posteriores

Ángulos en rectas paralelas Ángulos alternos Ángulos correspondientes Ángulos colaterales Ángulos opuestos por el vértice Ángulos exteriores correspondientes Ángulos alternos internos Rectas perpendiculares

Practica por Tipo de Pregunta

Elige tu estilo de aprendizaje y formato de práctica preferido para problemas de fracciones

Generar un ángulo aleatorio Identificando y definiendo elementos Tres líneas paralelas Triángulo isósceles Usando formas geométricas adicionales Uso de ángulos en un triángulo Uso de variables