Recordemos la definición de ángulos correspondientes:
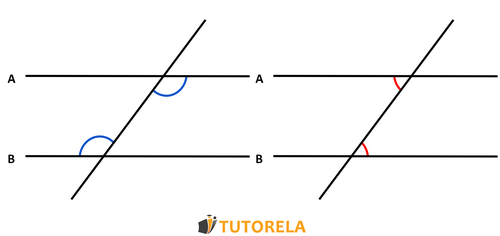
Los ángulos correspondientes son ángulos situados en el mismo lado de la recta que corta a las dos paralelas y también están situados en el mismo nivel con respecto a la recta paralela a la que son adyacentes.
Parece que según esta definición estos son los ángulos marcados con la letra A.
Recordemos la definición de ángulos adyacentes:
Los ángulos adyacentes son ángulos cuya formación es posible en una situación en la que hay dos rectas que se cruzan.
Estos ángulos se forman en el punto donde se produce la intersección, uno al lado del otro, y de aquí también proviene su nombre.
Los ángulos adyacentes siempre se complementan en ciento ochenta grados, es decir, su suma es 180 grados.
Parece que según esta definición estos son los ángulos marcados con la letra B.
Respuesta:
A- correspondientes B- adyacentes