Antes de profundizar en el tema de los ángulos opuestos por el vértice, nos detendremos un poco para visualizar bajo qué tipo de escenario pueden surgir este tipo de ángulos. Para facilitar su comprensión dibujaremos dos líneas rectas paralelas cortadas por una secante o transversal, tal como se ve en la siguiente ilustración:
Ejercicios de Ángulos en Rectas Paralelas - Práctica Completa
Domina los ángulos opuestos por el vértice, correspondientes, alternos y colaterales con ejercicios resueltos paso a paso y problemas de práctica interactivos.
📚¿Qué aprenderás practicando ángulos en rectas paralelas?
- Identificar ángulos opuestos por el vértice y aplicar que son iguales
- Resolver problemas con ángulos correspondientes en rectas paralelas cortadas por transversal
- Calcular medidas de ángulos alternos internos y externos usando propiedades geométricas
- Aplicar la propiedad de ángulos colaterales que suman 180 grados
- Resolver ecuaciones algebraicas para encontrar valores de ángulos desconocidos
- Analizar figuras geométricas complejas como paralelogramos y trapecios usando ángulos
Entendiendo la Ángulos opuestos por el vértice
Explicación completa con ejemplos
¿Qué son los ángulos opuestos por el vértice?
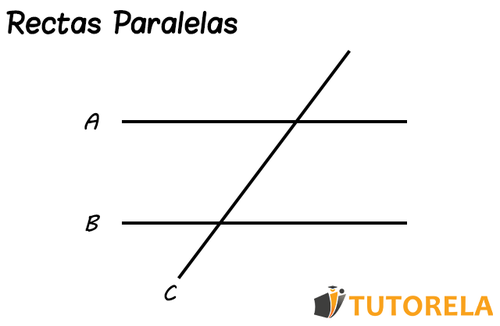
¿Qué es lo que vemos aquí? La transversal se cruza con cada una de las rectas y (en nuestro caso y son paralelas, pero eso no es indispensable para la formación de ángulos opuestos por el vértice).
Luego, apoyados de este ejemplo gráfico, estamos listos para pasar a la definición formal de los ángulos opuestos por el vértice, que nos ayudará a identificarlos con más facilidad:
Los ángulos opuestos por el vértice son un par de ángulos que surgen cuando dos rectas se cruzan. Estos ángulos se forman en el punto de intersección (al cuál llamaremos vértice), uno frente al otro. Los ángulos opuestos por el vértice son de idéntico tamaño.
En la siguiente ilustración podemos ver dos ejemplos de ángulos opuestos por el vértice, el primer par de ángulos opuestos por el vértice están marcados de color rojo y en el segundo par de color azul.
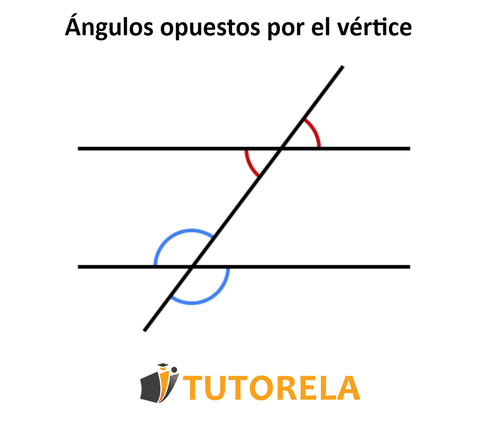
Practicar Ángulos opuestos por el vértice
Pon a prueba tus conocimientos con más de 48 cuestionarios
¿Cuáles ángulos en el dibujo son equiláteros?
Dado que a paralela a b
ejemplos con soluciones para Ángulos opuestos por el vértice
Soluciones paso a paso incluidas
Ejercicio #1
Las rectas en el dibujo son paralelas entre sí.
¿Qué ángulos se describen en la figura?
Solución Paso a Paso
Recordemos que los ángulos alternos se pueden definir como un par de ángulos que se pueden encontrar en el aspecto opuesto de una recta trazada para cortar dos líneas paralelas entre sí.
Además, estos ángulos se ubican en el nivel opuesto con respecto a la recta correspondiente a la que pertenecen.
Respuesta:
Alternos
Ejercicio #2
es paralela a
Determina cuál de las afirmaciones es correcta.
Solución Paso a Paso
Recuerda la definición de ángulos adyacentes:
Los ángulos adyacentes son ángulos cuya formación es posible en una situación en la que hay dos líneas rectas que se cruzan. Estos ángulos se forman en el punto donde se produce la intersección, uno contiguo al otro, y de aquí también sale su nombre.
Recuerda la definición de ángulos colaterales:
Dos ángulos formados cuando dos o más líneas paralelas son cortadas por una tercera línea. Los ángulos colaterales están del mismo lado de la línea de corte e incluso están a diferente altura en relación con la línea paralela a la que son adyacentes.
Por lo tanto, la respuesta C es correcta para esta definición.
Respuesta:
Colaterales Adyacentes
Solución en video
Ejercicio #3
¿En cuál de los dibujos hay ángulos opuestos por el vértice?
Solución Paso a Paso
Recuerda la definición de ángulos opuestos por el vértice:
Los ángulos opuestos por el vértice son ángulos cuya formación es posible cuando dos rectas se cruzan, y se forman en el punto de intersección, una enfrentada a la otra. Los ángulos agudos son iguales en tamaño.
El dibujo de la respuesta A corresponde a esta definición.
Respuesta:
Solución en video
Ejercicio #4
¿Es posible tener dos ángulos adyacentes, uno de los cuales sea obtuso y el otro recto?
Solución Paso a Paso
Recuerda la definición de ángulos adyacentes:
Los ángulos adyacentes siempre se complementan hasta ciento ochenta grados, es decir, su suma es 180 grados.
Esta situación es imposible ya que un ángulo recto es igual a 90 grados, un ángulo obtuso es mayor a 90 grados.
Por lo tanto, en conjunto su suma será mayor que 180 grados.
Respuesta:
Falso
Solución en video
Ejercicio #5
¿Qué ángulos se describen en el dibujo?
Solución Paso a Paso
Como los ángulos no están en líneas paralelas, ninguna de las respuestas es correcta.
Respuesta:
Ninguna de las respuestas
Preguntas Frecuentes
¿Cómo identifico si dos ángulos son opuestos por el vértice?
+Los ángulos opuestos por el vértice se forman cuando dos rectas se cruzan, creando cuatro ángulos en el punto de intersección. Los ángulos que están uno frente al otro (sin compartir lado común) son opuestos por el vértice y siempre miden lo mismo.
¿Cuál es la diferencia entre ángulos correspondientes y alternos?
+Los ángulos correspondientes están en el mismo lado de la transversal y en la misma posición relativa respecto a cada recta paralela. Los ángulos alternos están en lados opuestos de la transversal y en posiciones diferentes respecto a las rectas paralelas.
¿Por qué los ángulos colaterales suman 180 grados?
+Los ángulos colaterales están en el mismo lado de la transversal pero en niveles diferentes respecto a las rectas paralelas. Como forman una línea recta cuando se unen, su suma siempre es 180° (ángulos suplementarios).
¿Cómo resolver problemas de ángulos en paralelogramos usando vértices?
+En un paralelogramo, las diagonales se intersectan formando ángulos opuestos por el vértice. Usa esta propiedad junto con la suma de ángulos en triángulos (180°) para encontrar medidas desconocidas en los triángulos formados.
¿Qué propiedades de ángulos se aplican en rectas paralelas?
+Las principales propiedades son: 1) Ángulos correspondientes son iguales, 2) Ángulos alternos internos/externos son iguales, 3) Ángulos colaterales suman 180°, 4) Ángulos opuestos por el vértice son iguales.
¿Cómo planteo ecuaciones para resolver ángulos desconocidos?
+Identifica la relación entre los ángulos (iguales, suplementarios, etc.), establece la ecuación usando las propiedades conocidas, y despeja la variable. Por ejemplo: si dos ángulos son opuestos por el vértice, iguala sus expresiones algebraicas.
¿Cuándo uso ángulos en rectas paralelas en la vida real?
+Se aplican en arquitectura para diseñar estructuras paralelas, en navegación para calcular rumbos, en ingeniería para construir puentes y carreteras, y en diseño gráfico para crear perspectivas y patrones geométricos.
¿Qué errores comunes debo evitar al resolver estos problemas?
+Errores frecuentes incluyen: confundir tipos de ángulos, no identificar correctamente las rectas paralelas, olvidar que ángulos opuestos por el vértice son iguales, y no verificar que ángulos colaterales sumen 180°.