La descomposición en factores primos (o descomposición factorial) consiste en descomponer cierto número en números primos, llamados factores, cuyo producto (multiplicación) tenga como resultado el número original.
Ejercicios de Descomposición en Factores Primos - Práctica
Practica la factorización prima con ejercicios paso a paso. Aprende el método del árbol de factores y división. Ideal para estudiantes de matemáticas.
📚Domina la Descomposición en Factores Primos con Ejercicios Interactivos
- Aplica el método del árbol de factores para descomponer números compuestos
- Utiliza el método de ventana de división para encontrar factores primos
- Identifica números primos y compuestos correctamente en cada paso
- Resuelve problemas de factorización desde números simples hasta complejos
- Verifica tus respuestas comparando diferentes métodos de descomposición
- Desarrolla estrategias para encontrar el factor primo más pequeño
Entendiendo la Descomposición en números primos
Explicación completa con ejemplos
Descomposición en factores primos
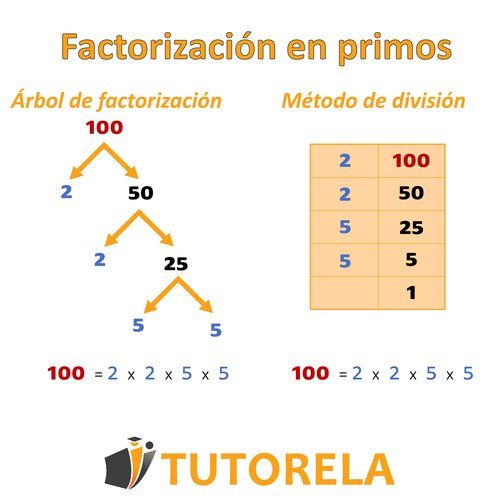
El primer modo - Método del árbol de factores
Tomemos el número que deseamos descomponer en factores y saquémosle ramas.
Nos preguntaremos, qué números podemos encontrar cuya multiplicación tenga como resultado este mismo número, a excepción del número original y del .
Miremos si los números que hallamos son primos o compuestos, a los compuestos los volveremos a descomponer en dos ramas.
Seguiremos descomponiendo todos los números compuestos hasta llegar sólo a primos, los señalaremos con un círculo.
El segundo modo - Método de ventana de división
Escribamos el número que deseamos descomponer en factores a la izquierda de una raya vertical que actúa como ventana de división.
Busquemos el número primo más pequeño por el cual podamos dividir el original, lo escribimos a la derecha de la raya y el resultado lo escribiremos a la izquierda, debajo del primero. Seguiremos de este modo hasta llegar al número y terminar el ejercicio.
Todos los números primos aparecerán a la derecha de la raya divisora.
Practicar Descomposición en números primos
Pon a prueba tus conocimientos con más de 8 cuestionarios
Escriba todos los factores del siguiente número: \( 99 \)
ejemplos con soluciones para Descomposición en números primos
Soluciones paso a paso incluidas
Ejercicio #1
Escriba todos los factores del siguiente número:
Solución Paso a Paso
Respuesta:
Solución en video
Ejercicio #2
Escriba todos los factores del siguiente número:
Solución Paso a Paso
Respuesta:
Solución en video
Ejercicio #3
Escriba todos los factores del siguiente número:
Solución Paso a Paso
Respuesta:
No hay factores primos
Solución en video
Ejercicio #4
Escriba todos los factores del siguiente número:
Solución Paso a Paso
Respuesta:
Solución en video
Ejercicio #5
Escriba todos los factores del siguiente número:
Solución Paso a Paso
Respuesta:
No hay factores primos
Solución en video
Preguntas Frecuentes
¿Cuál es la diferencia entre el método del árbol y el método de división?
+El método del árbol descompone el número en dos factores a la vez, creando ramas hasta llegar a números primos. El método de división usa una línea vertical y divide repetidamente por el número primo más pequeño posible hasta llegar a 1.
¿Cómo sé si un número es primo o compuesto durante la factorización?
+Un número primo solo se divide entre 1 y él mismo (como 2, 3, 5, 7). Un número compuesto tiene más divisores y se puede descomponer en factores más pequeños. En el árbol, los primos se marcan con círculos.
¿Qué hago si no encuentro factores para un número?
+Si no puedes encontrar factores diferentes a 1 y el número mismo, entonces ese número es primo. Márcalo con un círculo en el árbol o úsalo como factor final en el método de división.
¿El orden de los factores primos afecta el resultado final?
+No, el producto de los factores primos siempre será el mismo número original, sin importar el orden. Por ejemplo: 2×2×3×5 = 3×2×5×2 = 60.
¿Cuáles son los números primos más comunes que debo recordar?
+Los números primos más utilizados en factorización son: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29. Memorizar estos te ayudará a factorizar más rápidamente.
¿Cómo verifico si mi descomposición en factores primos es correcta?
+Multiplica todos los factores primos que obtuviste. El resultado debe ser igual al número original. También puedes usar ambos métodos (árbol y división) para confirmar que obtienes los mismos factores.
¿Qué números son más difíciles de factorizar?
+Los números con factores primos grandes son más desafiantes. Números como 77 (7×11) o 91 (7×13) requieren probar varios números primos. Los números con muchos factores pequeños como 64 (2⁶) son más fáciles.
¿Puedo usar calculadora para la descomposición en factores primos?
+Aunque puedes usar calculadora para las divisiones, es importante practicar mentalmente para desarrollar habilidades matemáticas. La calculadora es útil para verificar resultados en números muy grandes.