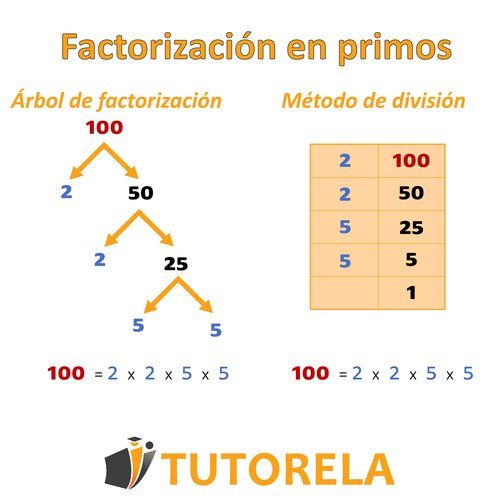
La descomposición en factores primos (o descomposición factorial) consiste en descomponer cierto número en números primos, llamados factores, cuyo producto (multiplicación) tenga como resultado el número original.
Descomposición en factores primos
Descomposición en factores primos
El primer modo - Método del árbol de factores
Tomemos el número que deseamos descomponer en factores y saquémosle ramas.
Nos preguntaremos, qué números podemos encontrar cuya multiplicación tenga como resultado este mismo número, a excepción del número original y del .
Miremos si los números que hallamos son primos o compuestos, a los compuestos los volveremos a descomponer en dos ramas.
Seguiremos descomponiendo todos los números compuestos hasta llegar sólo a primos, los señalaremos con un círculo.
El segundo modo - Método de ventana de división
Escribamos el número que deseamos descomponer en factores a la izquierda de una raya vertical que actúa como ventana de división.
Busquemos el número primo más pequeño por el cual podamos dividir el original, lo escribimos a la derecha de la raya y el resultado lo escribiremos a la izquierda, debajo del primero. Seguiremos de este modo hasta llegar al número y terminar el ejercicio.
Todos los números primos aparecerán a la derecha de la raya divisora.
¡Pruébate en descomposición en números primos!
Escriba todos los factores del siguiente número: \( 6 \)
Descomposición en factores primos
En este artículo aprenderás a descomponer cualquier número en factores primos ¡con la ayuda de dos magníficos trucos que seguro amarás!
¿Qué es la descomposición en factores (o la factorización)?
La descomposición en factores (factorizacióno descomposición factorial) es la descomposición de cierto número en números más pequeños - primos, cuyo producto (multiplicación) sea el número original.
Luego de haber aprendido qué es un número compuesto y un número primo, aprenderemos aquí cómo descomponer un número compuesto en factores primos.
Escriba todos los factores del siguiente número: \( 7 \)
Escriba todos los factores del siguiente número: \( 5 \)
Escriba todos los factores del siguiente número: \( 9 \)
El primer modo - Método del árbol de factores
Tomaremos el número que deseamos descomponer en factores y le sacaremos ramas.
Por ejemplo:

Nos preguntaremos, qué números podemos encontrar cuya multiplicación tenga como resultado este mismo número, a excepción del número original y del .
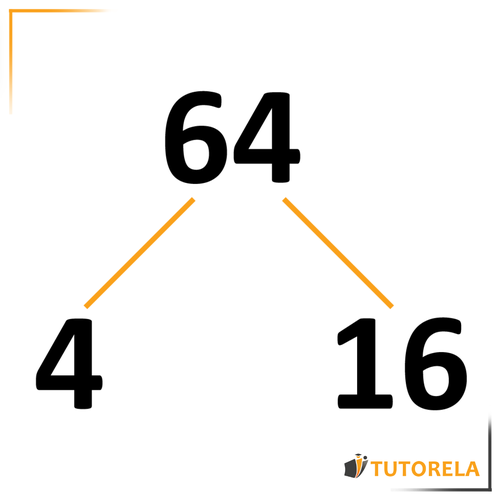
En este ejemplo elegiremos los números y .
Observa que, podríamos haber elegido todo par de números cuyo producto fuese y, de todos modos, habríamos llegado al mismo resultado.
Anotaremos el y el debajo de las ramas del siguiente modo:
Ahora averiguaremos si y son números compuestos. Nuevamente buscaremos números cuyo producto dé o .
¡Atención! Esto es válido a excepción del número en sí y del .
Al número podemos encontrarle el y eו
Al número podemos encontrarle el y el
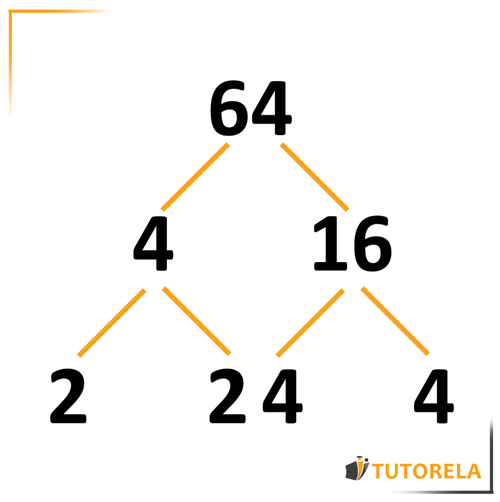
Nuevamente extraeremos ramas de cada número y escribiremos los factores del siguiente modo:
Ahora seguiremos preguntando
¿ es un número primo?
Sí.
¿ es un número primo?
No. Podemos seguir sacándole factores y .
Por consiguiente, continuaremos con el árbol del lado derecho y señalaremos con un círculo todos los factores que son números primos.
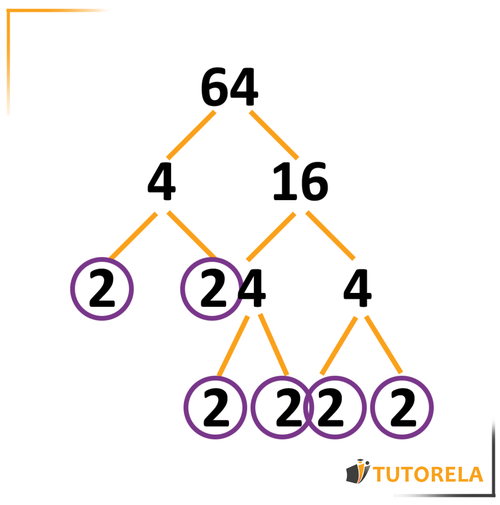
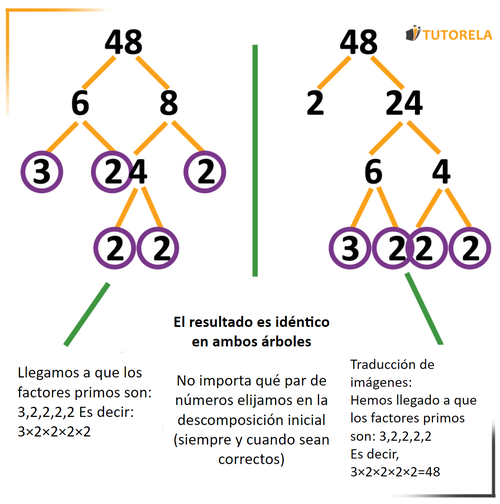
¿Qué conseguimos?
Si descomponemos a en factores primos nos dará que:
son los factores primos de .
Otro ejemplo
Tomemos el número y veamos cómo llegamos al mismo resultado incluso si comenzamos a descomponerlo con factores diferentes:
A la derecha, descompondremos a como el producto de y. A la izquierda, descompondremos a como el producto de y .
Seguiremos según los pasos de operación
A la derecha, sólo descompondremos a . es primo, por lo tanto, lo marcaremos con un círculo.
A la izquierda, descompondremos a y también a .
Seguiremos descomponiendo todos los números compuestos hasta llegar sólo a primos, los señalaremos con un círculo.
Escriba todos los factores del siguiente número: \( 8 \)
Escribe los factores primos del siguiente número: \( 4 \)
Escriba todos los factores del siguiente número: \( 16 \)
El segundo modo: Método de ventana de división
Escribamos el número que deseamos descomponer en factores a la izquierda de una raya vertical que actúa como ventana de división.
Busquemos el número primo más pequeño por el cual podamos dividir el original, lo escribimos a la derecha de la raya y el resultado lo escribiremos a la izquierda, debajo del primero. Seguiremos de este modo hasta llegar al número y terminar el ejercicio.
Todos los números primos aparecerán a la derecha de la raya divisora.
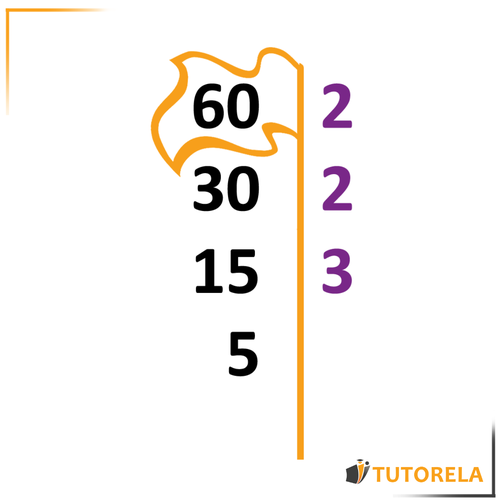
Veámoslo ejercitando: Descompondremos el número en factores primos:
Nos preguntaremos ¿cuál es el número primo más pequeño por el cual podamos dividirlo? La respuesta es . es un número primo y se divide por él.
Anotaremos frente al número a la derecha de la raya divisora.
Calculemos
Anotaremos el cociente (resultado de la división) debajo del número original, de la siguiente manera:

Ahora, seguiremos cuestionando: ¿Cuál es el número primo más pequeño que divide a ?
La respuesta es .
Volveremos a escribir a la derecha y anotaremos el cociente a la izquierda:

Ahora, seguiremos cuestionando: ¿Cuál es el número primo más pequeño que divide a ?
La respuesta es . Lo escribiremos a la derecha y el cociente a la izquierda.
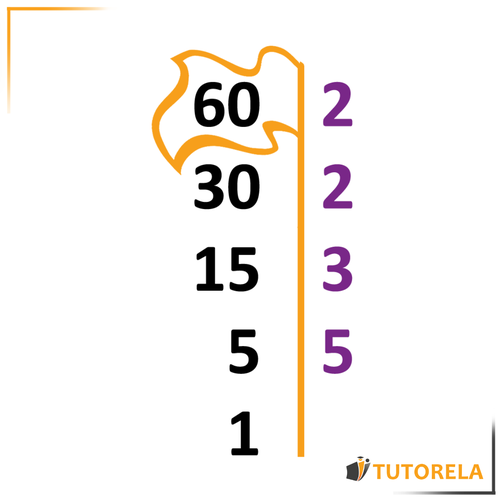
Ahora, seguiremos cuestionando: ¿Cuál es el número primo más pequeño que divide a ?
La respuesta es .
Lo anotaremos a la derecha y el resultado a la izquierda.
Llegamos al número , que no se puede descomponer.
Eso quiere decir que hemos finalizado el ejercicio y los factores primos son los que aparecen del lado derecho.
Es decir:
Ejemplos y ejercicios con soluciones de descomposición en factores primos
Ejercicio #1
Escriba todos los factores del siguiente número:
Solución en video
Respuesta
Ejercicio #2
Escriba todos los factores del siguiente número:
Solución en video
Respuesta
No hay factores primos
Ejercicio #3
Escriba todos los factores del siguiente número:
Solución en video
Respuesta
No hay factores primos
Ejercicio #4
Escriba todos los factores del siguiente número:
Solución en video
Respuesta
Ejercicio #5
Escriba todos los factores del siguiente número:
Solución en video
Respuesta
Escriba todos los factores del siguiente número: \( 12 \)
Escriba todos los factores del siguiente número: \( 13 \)
Escriba todos los factores del siguiente número: \( 14 \)
- Orden de operaciones básicas: suma, resta, multiplicación y división
- Orden de las operaciones básicas (potencias)
- Orden de operaciones básicas: raíces
- El 0 y el 1 en el orden de las operaciones
- Inverso multiplicativo
- Orden de las operaciones: paréntesis
- La propiedad conmutativa
- La propiedad asociativa
- Cómo calcular el área de un ortoedro
- Potenciación de números enteros
- Las Tablas de Multiplicar
- Fracciones









