Los triángulos semejantes son triángulos para los que existe cierta razón de semejanza, es decir, cada uno de los lados de un triángulo está en una proporción uniforme con respecto al lado correspondiente en el otro triángulo. Además, los ángulos en las mismas ubicaciones también son iguales para los dos triángulos similares.
Ejercicios de Triángulos Semejantes - Práctica y Problemas
Domina los triángulos semejantes con ejercicios paso a paso. Aprende criterios AA, LAL, LLL, razón de semejanza y cálculo de áreas. Práctica gratis online.
📚Practica y Domina los Triángulos Semejantes
- Identifica triángulos semejantes usando los criterios AA, LAL y LLL
- Calcula la razón de semejanza entre triángulos correspondientes
- Resuelve problemas de perímetros y áreas en triángulos semejantes
- Aplica las propiedades de semejanza para encontrar lados desconocidos
- Demuestra la semejanza de triángulos usando teoremas geométricos
- Relaciona la razón de semejanza con la razón de áreas y perímetros
Entendiendo la Triángulos semejantes
Explicación completa con ejemplos
¿Qué es la semejanza de triángulos?
¿Cómo se demuestra la semejanza de los triángulos?
Para probar la semejanza de triángulos es común utilizar uno de los tres teoremas:
- Ángulo-ángulo (es decir, dos pares de ángulos iguales en triángulos)
- Lado-ángulo-lado (relación de semejanza de dos pares de lados en triángulos y los ángulos atrapados entre ellos son iguales)
- Lado-lado-lado (relación de semejanza de tres pares de lados en triángulos)
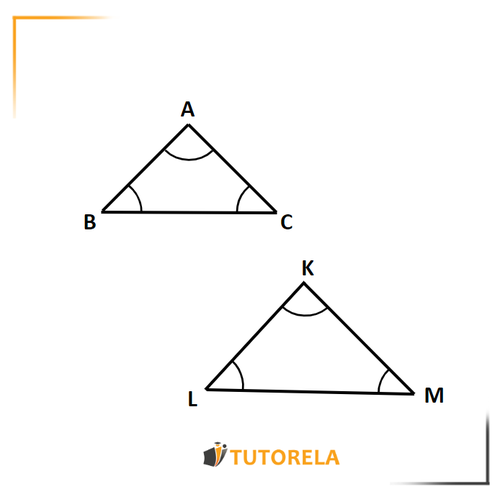
Las semejanzas de triángulos se expresan con el signo .
Practicar Triángulos semejantes
Pon a prueba tus conocimientos con más de 9 cuestionarios
Dados los dos triángulos siguientes:
Dado que los ángulos B y F son iguales
Ángulo C es igual al ángulo D
¿Cuál lado corresponde a AB?
ejemplos con soluciones para Triángulos semejantes
Soluciones paso a paso incluidas
Ejercicio #1
Dados los dos siguientes triángulos
Dado que los ángulos B y D son iguales.
El ángulo A es igual al F
¿Qué lado corresponde al lado AB?
Solución Paso a Paso
Como tenemos dos ángulos iguales, usaremos el teorema ángulo-ángulo para simular triángulos.
Compararemos los vértices
Según los datos parece que:
El lado AC corresponde al lado EF
El lado BC corresponde al lado DE
Por lo tanto el lado AB corresponde al lado FD
Respuesta:
Solución en video
Ejercicio #2
Dados los dos triángulos siguientes
Dado que el ángulo B es igual al ángulo E
El ángulo A es igual al ángulo D
¿Qué ángulo corresponde al ángulo C?
Solución Paso a Paso
Como tenemos dos pares de ángulos correspondientes, usaremos el teorema ángulo-ángulo para semejanza de triángulos.
Ahora que sabemos que todos los ángulos son iguales entre sí, notaremos que el ángulo que nos queda que es igual y corresponde al ángulo C es el ángulo F.
Respuesta:
Solución en video
Ejercicio #3
Dado:
Ángulo B es igual a 40°
Ángulo C es igual a 60°
Ángulo E es igual a 40°
Ángulo F es igual a 60°
¿Los triángulos son semejantes?
Solución Paso a Paso
Dado que los datos muestran que hay dos pares de ángulos iguales:
Basta demostrar que los triángulos son semejantes mediante el teorema del ángulo - ángulo.
Por lo tanto, el triángulo ABC es semejante al triángulo DEF
Respuesta:
Si
Solución en video
Ejercicio #4
Dado:
El ángulo B es igual a 70 grados
El ángulo C es igual a 35 grados
El ángulo E es igual a 70 grados
El ángulo F es igual a 35 grados
¿Los triángulos son semejantes?
Solución Paso a Paso
De hecho, los triángulos son semejantes según el teorema ángulo-ángulo.
Dos pares de ángulos iguales son suficientes para afirmar que los triángulos son semejantes.
Respuesta:
Si
Solución en video
Ejercicio #5
Dados los dos siguientes triángulos:
Dado que el ángulo B es igual al ángulo F
Ángulo C es igual al ángulo D
¿Qué ángulo corresponde al ángulo A?
Solución Paso a Paso
Usamos el teorema ángulo-ángulo para simular triángulos.
Observemos los datos que ya tenemos:
Dado que los ángulos B y F son iguales
El ángulo C es igual al D
Por lo tanto lo que queda: los ángulos A y E son iguales.
Respuesta:
Solución en video
Preguntas Frecuentes
¿Cuáles son los 3 criterios para demostrar que dos triángulos son semejantes?
+Los tres criterios de semejanza son: 1) Ángulo-Ángulo (AA): dos pares de ángulos iguales, 2) Lado-Ángulo-Lado (LAL): razón igual de dos pares de lados y ángulo incluido igual, 3) Lado-Lado-Lado (LLL): razón igual de los tres pares de lados correspondientes.
¿Cómo se calcula la razón de semejanza entre triángulos?
+La razón de semejanza se calcula dividiendo la longitud de cualquier lado de un triángulo entre la longitud del lado correspondiente del otro triángulo. Por ejemplo, si un lado mide 12 cm y su correspondiente mide 8 cm, la razón es 12/8 = 3/2 = 1.5.
¿Cuál es la diferencia entre triángulos semejantes y congruentes?
+Los triángulos semejantes tienen la misma forma pero pueden tener diferentes tamaños (lados proporcionales). Los triángulos congruentes tienen la misma forma Y el mismo tamaño (lados y ángulos exactamente iguales).
¿Cómo se relaciona la razón de semejanza con el área de los triángulos?
+Si la razón de semejanza entre dos triángulos es k, entonces la razón entre sus áreas es k². Por ejemplo, si la razón de semejanza es 3, la razón de áreas será 3² = 9.
¿Qué significa que dos triángulos tengan una razón de semejanza de 2:1?
+Significa que cada lado del triángulo mayor es exactamente el doble del lado correspondiente en el triángulo menor. También significa que el área del triángulo mayor es 4 veces mayor (2² = 4) y el perímetro es 2 veces mayor.
¿Cómo encontrar un lado desconocido en triángulos semejantes?
+Primero establece la razón de semejanza usando lados conocidos, luego aplica esta razón al lado desconocido. Si la razón es 3:2 y necesitas encontrar un lado x que corresponde a un lado de 15, entonces x/15 = 2/3, por lo que x = 10.
¿Los triángulos semejantes siempre tienen los mismos ángulos?
+Sí, los triángulos semejantes siempre tienen ángulos correspondientes iguales. Esta es una propiedad fundamental: si dos triángulos son semejantes, sus ángulos correspondientes son congruentes (iguales en medida).
¿Qué aplicaciones tienen los triángulos semejantes en la vida real?
+Los triángulos semejantes se usan para medir alturas inaccesibles (usando sombras), en mapas y planos (escalas), en fotografía (proporciones), en arquitectura y construcción, y en navegación para calcular distancias.