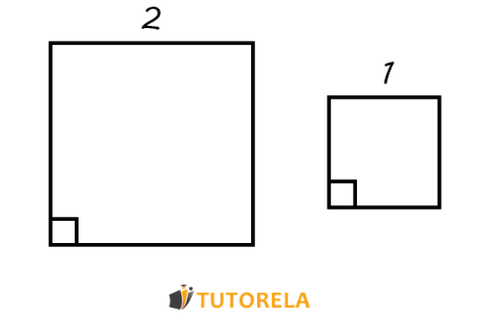
La semejanza entre figuras geométricas se cumple cuando éstas tienen ángulos del mismo tamaño respectivamente y también hay proporcionalidad entre los lados de dichas figuras.
De un modo intuitivo, igual que como ocurre con los triángulos, dos figuras semejantes son, de hecho, una ampliación de la otra.
Se sabe que los dos polígonos son semejantes, encuentra los otros lados del polígono ABCD.
¿Es el rectángulo ABCD semejante al rectángulo EFGH?
Intentamos comprobar la razón de semejanza.
Examinamos si:
Reemplazamos los datos:
La razón no es igual, por lo que los rectángulos no son semejantes.
Respuesta:
No semejantes
Dados dos rectángulos semejantes, halla el perímetro del rectángulo más grande.
Recordemos que en un rectángulo hay dos pares de lados paralelos e iguales.
Llamaremos al triángulo pequeño 1 y al triángulo grande 2.
Calculamos el perímetro del triángulo pequeño:
Puesto que sabemos que los rectángulos son semejantes:
Colocamos los datos que conocemos para el perímetro:
Respuesta:
40 cm
Aquí hay dos paralelogramos semejantes.
La razón entre los lados es 3:4.
¿Cuál es la razón del área del paralelogramo?
El cuadrado de la razón entre los lados es igual a la razón entre las áreas de los paralelogramos:
Respuesta:
9:16
Frente a ti hay dos hexágonos con una razón de semejanza ¿qué ángulos son correspondientes?
Respuesta:
Ángulo C = Ángulo O
Elija la respuesta correcta
Respuesta:
Los rectángulos son semejantes