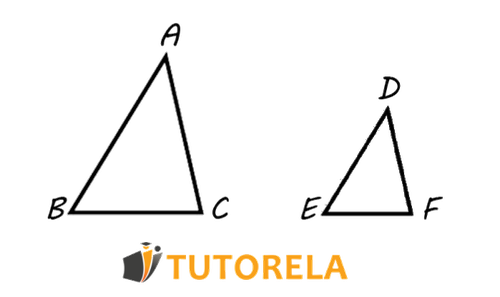
Los triángulos semejantes son triángulos cuyos tres ángulos son iguales respectivamente y además la razón entre cada par de lados correspondientes es igual. Dos triángulos semejantes, en realidad se están agrandando o reduciendo el uno al otro.
La razón de semejanza es la razón entre dos lados correspondientes en dos triángulos semejantes.
Para demostrar semejanzas entre triángulos, usaremos los siguientes teoremas:
- Ángulo-Ángulo (A.A): Si dos ángulos son iguales respectivamente entre dos triángulos, entonces los triángulos son semejantes.
- Lado-Ángulo-Lado (L.A.L): Si la razón de dos pares de lados es igual, y también los ángulos comprendidos entre ellos son iguales entre sí, entonces los triángulos son semejantes.
- Lado-Lado-Lado (L.L.L): Si para dos triángulos, la razón de los tres lados en un triángulo a los tres pares en el otro triángulo es igual (razón de semejanza), entonces los triángulos son semejantes.
Para semejanza de poligonos lo definiremos de esta manera: si para dos polígonos todos los ángulos son iguales y hay una razón constante entre dos lados correspondientes, entonces los polígonos son semejantes.
Intuitivamente, al igual que los triángulos semejantes, también dos polígonos semejantes son en realidad una ampliación o reducción entre sí.