Triángulos semejantes

Los triángulos semejantes son triángulos para los que existe cierta razón de semejanza, es decir, cada uno de los lados de un triángulo está en una proporción uniforme con respecto al lado correspondiente en el otro triángulo. Además, los ángulos en las mismas ubicaciones también son iguales para los dos triángulos similares. 

Para probar la semejanza de triángulos es común utilizar uno de los tres teoremas: 

• Ángulo-ángulo (es decir, dos pares de ángulos iguales en triángulos)
• Lado-ángulo-lado (relación de semejanza de dos pares de lados en triángulos y los ángulos atrapados entre ellos son iguales)
• Lado-lado-lado (relación de semejanza de tres pares de lados en triángulos)

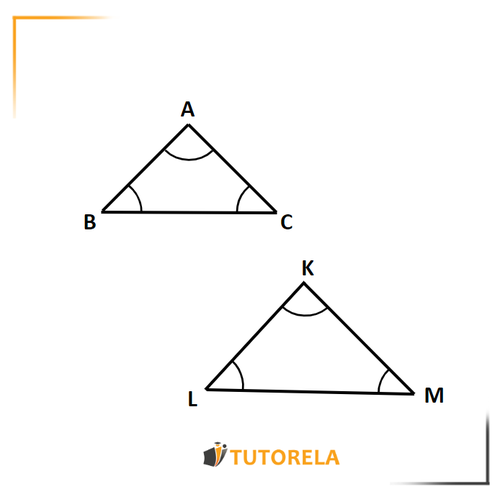
Las semejanzas de triángulos se expresan con el signo $∼$. 

Ilustraremos la cuestión con un ejemplo. 

El dibujo que tenemos ante nosotros muestra dos triángulos semejantes,$\triangle ABC$ y $\triangle KLM$.

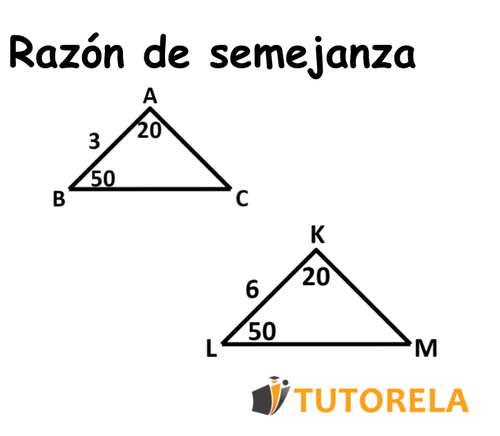
La razón de semejanza de los triángulos es $2$. Esto significa que cada lado en el triángulo más grande $\triangle ABC$ es dos veces más grande que el lado correspondiente en el triángulo más pequeño $\triangle KLM$. 

Además, los ángulos en los lugares correspondientes en los dos triángulos son iguales entre sí. 

Como se ilustra en el dibujo, se cumple lo siguiente:

El ángulo $\sphericalangle A$ es igual al ángulo $\sphericalangle K$
El ángulo $\sphericalangle B$ es igual al ángulo $\sphericalangle L$
El ángulo $\sphericalangle C$ es igual al ángulo $\sphericalangle M$

Si te interesa este artículo también te pueden interesar los siguientes artículos

• Semejanza de triángulos y polígonos
• Razón de semejanza
• Criterio de semejanza entre dos triángulos
• Semejanza de figuras geométricas

En el blog de Tutorela encontrarás una gran variedad de artículos de matemáticas

Consigna

Si estamos hablando de triángulos semejantes entonces:

Elija la respuesta correcta.

Solución

En triángulos semejantes, la razón entre las longitudes de los lados de dos triángulos semejantes es igual a la razón entre sus perímetros.

Respuesta

La razón de las longitudes de los lados de dos triángulos es igual a la razón de sus perímetros

La razón entre el área de los triángulos semejantes es $\frac{9}{100}$.

Si nos dan que el perímetro del triángulo grande es $129\operatorname{cm}$, ¿Cuál es el perímetro del triángulo pequeño?

Solución

$\frac{S\triangle}{S\triangle}=\frac{9}{100}$

La razón entre los lados es

$\frac{3}{10}$

$\frac{P\triangle}{P\triangle}=\frac{P\triangle}{129}=\frac{3}{10}$

El perímetro del triángulo pequeño es $38.7$

Respuesta

$38.7$

Consigna

Dados dos triángulos semejantes. El área del triángulo pequeño es $12.5$, ¿Cuál es la longitud del lado?

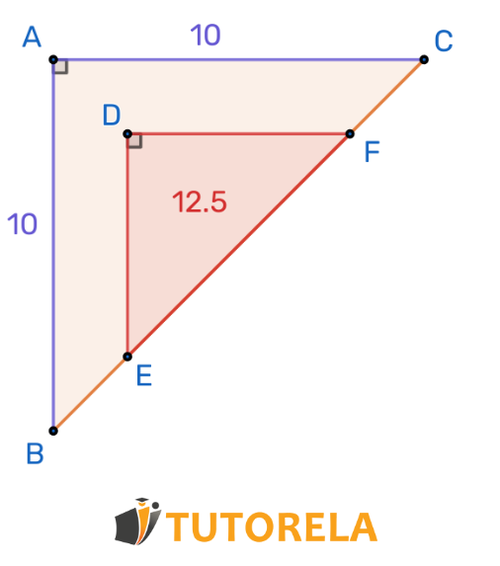
Área del triángulo grande

$\frac{10\times10}{2}=50$

El área del triángulo pequeño es $12.5$

$\frac{50}{12.5}=4$

$\sqrt{4}=2$

$\frac{10}{x}=2$

$x=5$

Respuesta

$5$

Consigna

Cuál es el área del triángulo azul si se da que los dos triángulos son semejantes y el área del triángulo verde es $64$.

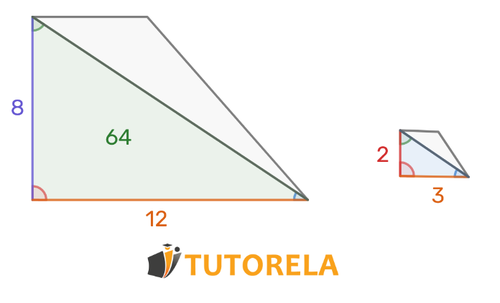
Solución

De la semejanza se deduce que $\frac{12}{3}=4$

$\frac{64}{S}=16$

$\frac{64}{16}=S$

$S=4$

Respuesta

$4$

Consigna

La razón de semejanza entre dos triángulos semejantes es $7$, entonces la razón de las áreas es $_{——}$

Solución

En general, esta consigna se basa en la "regla" simple: la razón del área es igual al cuadrado de la relación de semejanza

Entonces, si la razón de semejanza es $7$,

la razón de las áreas es $7^2$

que es $49$

Respuesta

$49$

¿Qué son dos triángulos semejantes?

Podemos decir que dos triángulos son semejantes cuando tienen la misma forma aunque tengan diferentes tamaños, para eso deben de cumplir con algunos de los criterios de semejanza.

¿Cuáles son los tres criterios de semejanza?

Para saber que dos triángulos son semejantes debe de cumplir con algunos de los tres criterios de semejanza:

• Lado-Lado-Lado (LLL): Si la razón de sus tres pares de lados correspondientes es la misma entonces dos triángulos son semejantes.
• Lado-Ángulo- Lado (LAL): Dos triángulos son semejantes si la razón de dos pares de lados correspondientes es la misma y el ángulo que está comprendido entre estos dos pares en el mismo, entonces serán triángulos semejantes.
• Ángulo-Ángulo (AA): Para que dos triángulos sean semejantes por este criterio, dos de sus ángulos respectivos deberán medir lo mismo y por ende el tercer ángulo también debe de tener la misma medida que el correspondiente a ese ángulo. Es decir, sus tres ángulos correspondientes miden lo mismo.

¿Qué es la razón de semejanza de dos triángulos?

Es el cociente de dividir los lados correspondientes de dichos triángulos.

¿Cómo sacar la razón de semejanza de dos triángulos?

La razón de semejanza se saca dividiendo los lados correspondientes de dos figuras semejantes, es este caso la de dos triángulos.

Veamos un ejemplo:

Consigna. Dado los siguientes triángulos semejantes $\triangle ABC\sim\triangle DEF$

Calcular la razón de semejanza

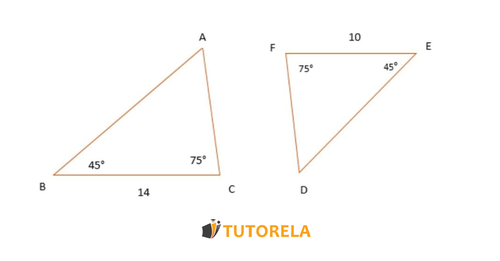
Dado que $\triangle ABC\sim\triangle DEF$ por el criterio de semejanza AA.

Entonces debemos de ubicar cuales son los lados correspondientes, y de aquí deducimos que

$\sphericalangle A=\sphericalangle D$

$\sphericalangle B=\sphericalangle E$

Entonces los lados correspondientes son $AB$ y $DE$

Ahora para calcular la razón de semejanza hacemos el cociente de estos dos lados.

$\frac{AB}{DE}=\frac{15}{10}=\frac{3}{2}=1.5$

Respuesta

$1.5$

¿Cuál es la diferencia entre dos triángulos semejantes y triángulos congruentes?

La diferencia es que cuando dos triángulos son semejantes tienen la misma forma pero no necesariamente deben de medir lo mismo los lados correspondientes, mientras que cuando dos triángulos son congruentes tienen la misma forma pero sus lados correspondientes miden lo mismo.

Ejercicio de semejanza de triángulos

Consigna. Demostrar que los siguientes triángulos son semejantes

De lo anterior podemos observar que tiene dos pares de ángulos iguales

$\sphericalangle B= 45°= \sphericalangle E$

$\sphericalangle C= 75°= \sphericalangle F$

Entonces decimos que los triángulos son semejantes por el criterio de semejanza AA. Tienen la misma forma pero en diferente posición.

Respuesta

$\triangle ABC\sim\triangle DEF$