Antes de profundizar en el tema de los ángulos opuestos por el vértice, nos detendremos un poco para visualizar bajo qué tipo de escenario pueden surgir este tipo de ángulos. Para facilitar su comprensión dibujaremos dos líneas rectas paralelas cortadas por una secante o transversal, tal como se ve en la siguiente ilustración:
Ángulos opuestos por el vértice
¿Qué son los ángulos opuestos por el vértice?
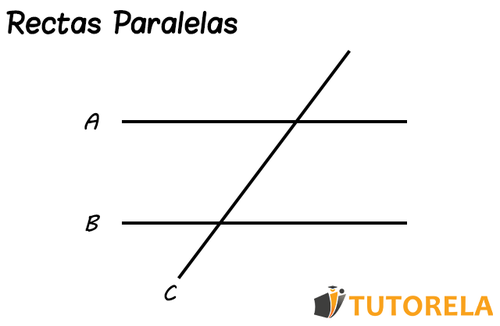
¿Qué es lo que vemos aquí? La transversal se cruza con cada una de las rectas y (en nuestro caso y son paralelas, pero eso no es indispensable para la formación de ángulos opuestos por el vértice).
Luego, apoyados de este ejemplo gráfico, estamos listos para pasar a la definición formal de los ángulos opuestos por el vértice, que nos ayudará a identificarlos con más facilidad:
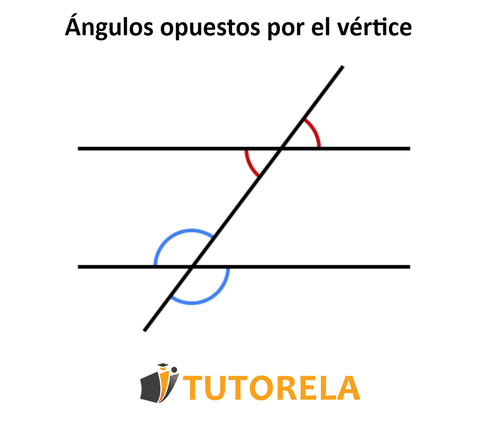
Los ángulos opuestos por el vértice son un par de ángulos que surgen cuando dos rectas se cruzan. Estos ángulos se forman en el punto de intersección (al cuál llamaremos vértice), uno frente al otro. Los ángulos opuestos por el vértice son de idéntico tamaño.
En la siguiente ilustración podemos ver dos ejemplos de ángulos opuestos por el vértice, el primer par de ángulos opuestos por el vértice están marcados de color rojo y en el segundo par de color azul.
¡Pruébate en ángulos sobre rectas paralelas!
¿El dibujo muestra un ángulo adyacente?
Más tipos de ángulos
Los ángulos opuestos por el vértice no son los únicos tipos de ángulos que podemos encontrar en diversos problemas geométricos. La ilustración descrita en la introducción convoca la aparición de varios tipos de ángulos que mencionaremos brevemente a continuación:
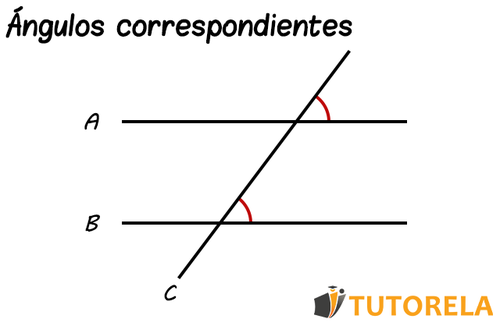
Ángulos correspondientes
Se les puede definir como un par de ángulos que podemos encontrar en el mismo lado de una transversal que corta dos rectas paralelas. Además, estos ángulos se encuentran en el mismo nivel respecto a la recta paralela a la cual pertenecen. Los ángulos correspondientes son de idéntico tamaño.
Si deseas recibir una explicación más amplia puedes consultar el artículo dedicado al tema «Ángulos correspondientes».
¿El dibujo muestra un ángulo adyacente?
¿El dibujo muestra un ángulo adyacente?
¿El dibujo muestra un ángulo adyacente?
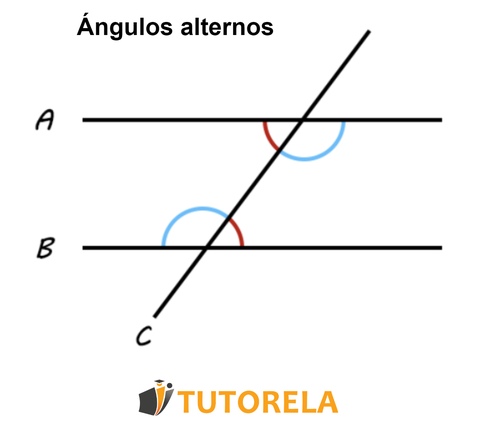
Ángulos alternos
Se les puede definir como un par de ángulos que podemos encontrar en lados opuestos de una transversal que corta dos rectas paralelas. Además, estos ángulos se encuentran en el nivel contrario respecto a la recta paralela a la cual pertenecen. Los ángulos alternos son de idéntico tamaño.
Si deseas recibir una explicación más amplia puedes consultar el artículo dedicado al tema «Ángulos alternos».
Ángulos colaterales
Se les puede definir como un par de ángulos que podemos encontrar en el mismo lado de una transversal que corta dos rectas paralelas. Además, estos ángulos se encuentran en el nivel contrario respecto a la recta paralela a la cual pertenecen. La suma de los ángulos colaterales equivale a .
Si deseas recibir una explicación más amplia puedes consultar el artículo dedicado al tema «Ángulos colaterales».
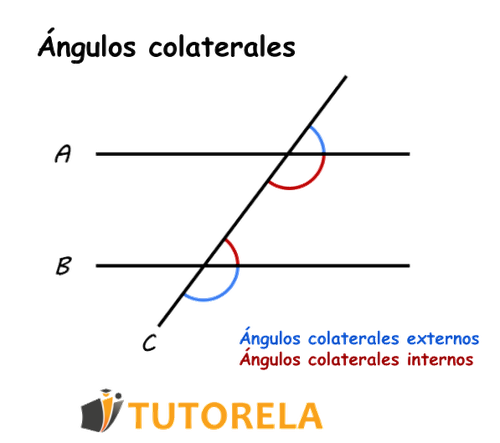
¿El dibujo muestra un ángulo adyacente?
¿El dibujo muestra un ángulo adyacente?
¿El dibujo muestra un ángulo adyacente?
Problemas de ejercitación con ángulos opuestos por el vértice
Ejercicio 1
En cada uno de los siguientes esquemas determina si los ángulos ilustrados son ángulos opuestos por el vértice y de no tener este tipo de ángulos especifica el tipo de ángulo del que se trata.
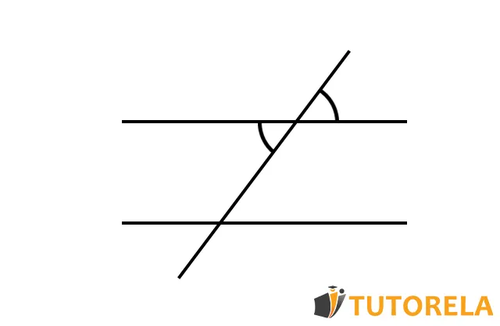
Esquema 1:
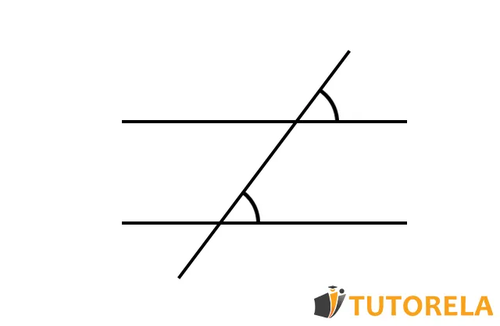
Esquema 2:
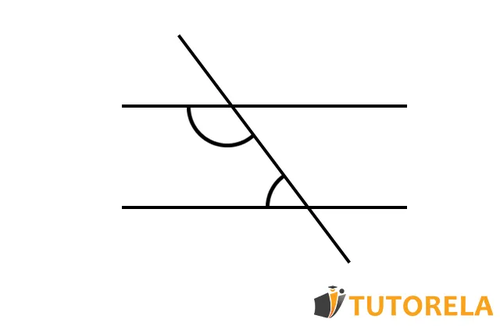
Esquema 3:
Solución:
Esquema 1:
En este esquema si se trata de ángulos opuestos por el vértice. La explicación es que responden al criterio de formación de dichos ángulos, es decir, dos rectas se cruzan y los ángulos opuestos por el vértice se forman en el punto de intersección, uno frente al otro.
Esquema 2:
En este esquema no se trata de ángulos opuestos por el vértice, sino de ángulos correspondientes. La explicación es que los dos ángulos se encuentran del mismo lado de la transversal que corta las dos rectas paralelas. Además, estos ángulos se encuentran en el mismo nivel respecto a la recta paralela a la cual pertenecen.
Esquema 3:
En este esquema tampoco se trata de ángulos opuestos por el vértice, sino de ángulos colaterales. La explicación es que los dos ángulos se encuentran del mismo lado de la transversal que corta las dos rectas paralelas. Además, estos ángulos se encuentran en el nivel contrario respecto a la recta paralela a la cual pertenecen.
Entonces:
Esquema 1: ángulos opuestos por el vértice
Esquema 2: ángulos correspondientes
Esquema 3: ángulos colaterales
Ejercicio 2
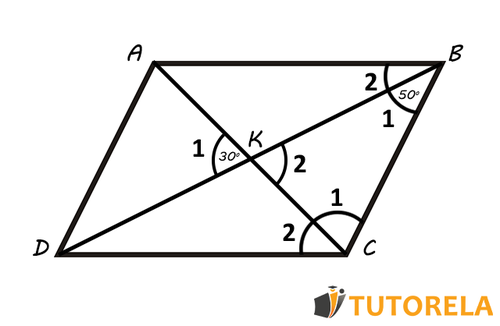
Dado el paralelogramo tal como se ve ilustrado en el esquema.
El punto es el punto de encuentro entre las diagonales en el paralelogramo .
El ángulo mide .
El ángulo mide . En base a la información dada hay que calcular el ángulo .
Solución:
Antes que nada, para ayudarnos a encontrar la respuesta, marcaremos los ángulos de la siguiente manera:
Nombraremos al ángulo (mide )
Nombraremos al ángulo
Nombraremos al ángulo (mide )
Nombraremos al ángulo (el ángulo buscado)
Primero, nos enfocaremos en el triángulo ya que el ángulo está en él.
Nos basaremos en lo que ya sabemos, la suma de los ángulos interiores de un triángulo es igual a . El ángulo mide por la información proporcionada. O sea, si pudiéramos encontrar la medida del ángulo , entonces podríamos calcular la del ángulo .
Como se deduce de los datos y del esquema, el punto es la intersección de las diagonales y en el paralelogramo . Entonces, podemos ver que acorde a su definición, este punto de intersección conforma los ángulos opuestos por el vértice y . Los ángulos opuestos por el vértice son del mismo tamaño, entonces .
Ahora podemos volver al triángulo y calcular el ángulo :
Es decir, el ángulo , que de hecho es el ángulo buscado mide .
Entonces:
El ángulo mide .
¿El dibujo muestra un ángulo adyacente?
¿El dibujo muestra un ángulo adyacente?
¿En cuál de los diagramas son los ángulos \( \alpha \) y \( \beta \) ángulos alternos?
Ejercicio 3
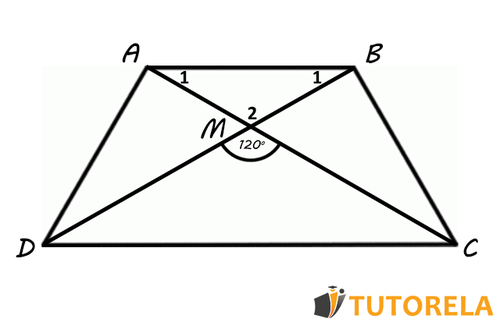
Dado el trapecio isósceles tal como se ve ilustrado en el esquema.
El punto es el punto de encuentro entre las diagonales del trapecio .
Ocurre que:
El ángulo mide .
Con base en la información dada, calcular los ángulos del triángulo .
Solución:
Antes que nada, para ayudarnos a encontrar la respuesta, marcaremos los ángulos de la siguiente manera:
Nombraremos al ángulo (mide )
Nombraremos al ángulo (ángulo buscado)
Nombraremos al ángulo (ángulo buscado)
Nombraremos al ángulo (ángulo buscado)
Nos enfocaremos en el triángulo ABM ya que debemos encontrar sus ángulos.
Comenzaremos con el ángulo .
Como se deduce de los datos y del esquema, el punto es la intersección de las diagonales y en el trapecio . Entonces, podemos ver que acorde a su definición, este punto de intersección conforma los ángulos opuestos por el vértice y . Los ángulos opuestos por el vértice son del mismo tamaño, por lo tanto, .
Ahora pasaremos a otro dato que tenemos, el lado . Este dato implica que el triángulo es un triángulo isósceles. Nos basaremos en el hecho que, en un triángulo isósceles los dos ángulos base tienen la misma medida.
Es decir,
Para descubrir su medida recordemos que, la suma de los ángulos interiores de un triángulo es y que la medida de ya la conocemos.
Por lo tanto, el cálculo nos dará:
Entonces:
El ángulo (ángulo ) mide .
El ángulo (ángulo ) mide .
El ángulo (ángulo ) mide .
Ejercicio 4
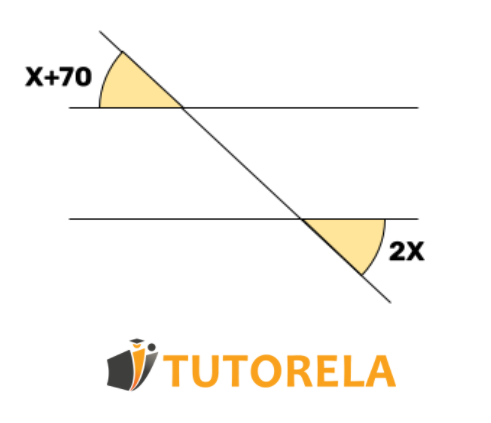
¿Cuál es el valor de sabiendo que las rectas son paralelas?
Solución:
Los ángulos marcados son ángulos externos a las rectas paralelas. Se puede utilizar nuestro conocimiento sobre los ángulos opuestos por el vértice, los cuales tienen los mismos datos.
Si tomamos uno de los ángulos opuestos por el vértice y el ángulo externo a las rectas paralelas restante vemos que en realidad son ángulos suplementarios y por lo tanto son iguales.
Es decir,
Entonces:
Encontramos que el valor de .
¿En cuál de las figuras hay ángulos? \( \alpha,\beta \) ¿Son ángulos opuestos por el vértice?
¿En cuál de las figuras hay ángulos? \( \alpha,\beta \) ¿Son ángulos opuestos por el vértice?
Puede haber una situación en la que haya dos ángulos adyacentes que sean rectos.
Ejercicio 5
Sabiendo que es paralela a , encontrar el valor de .
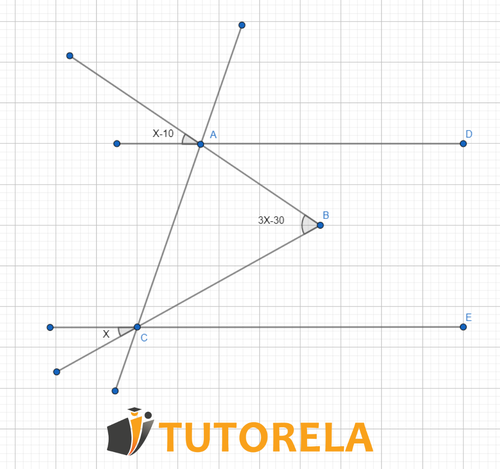
Solución:
Tenemos que el ángulo al ser opuesto por el vértice con el ángulo que mide . Un argumento similar nos lleva a que el ángulo .
Luego, por un resultado de rectas paralelas tenemos que , es decir, .
Entonces despejando el valor de tendríamos que
Entonces:
Preguntas de repaso:
¿Cuáles son los ángulos opuestos por el vértice?
Son ángulos que surgen cuando dos rectas se cruzan, uno frente al otro justo en el punto de intersección.
¿Cuál es la característica principal de los ángulos opuestos por el vértice?
La característica principal es que los ángulos opuestos por el vértice tienen el mismo valor.
¿En un esquema de rectas paralelas cortadas por una transversal, que par de ángulos tienen la misma propiedad de los ángulos opuestos por el vértice, es decir, que sean idénticos?
Los ángulos correspondientes y los ángulos alternos.
Si está interesado en aprender más sobre otros temas de ángulos, puede ingresar a uno de los siguientes artículos:
- Notación de ángulos
- Lados, vértices, y ángulos
- Bisectriz
- Ángulo recto
- Ángulos adyacentes
- Ángulos alternos
- Ángulos correspondientes
- Suma de los ángulos de un triángulo
- Suma de los ángulos de un polígono
En la página web de Tutorela encontrarás una variedad de artículos sobre matemáticas.
La suma de los ángulos adyacentes es 180 grados.
Si uno de los ángulos es recto, entonces el otro ángulo también será recto.
¿El dibujo muestra un ángulo adyacente?
ejemplos con soluciones para Ángulos opuestos por el vértice
Ejercicio #1
¿Es posible tener dos ángulos adyacentes, uno de los cuales sea obtuso y el otro recto?
Solución en video
Solución Paso a Paso
Recuerda la definición de ángulos adyacentes:
Los ángulos adyacentes siempre se complementan hasta ciento ochenta grados, es decir, su suma es 180 grados.
Esta situación es imposible ya que un ángulo recto es igual a 90 grados, un ángulo obtuso es mayor a 90 grados.
Por lo tanto, en conjunto su suma será mayor que 180 grados.
Respuesta
Falso
Ejercicio #2
¿En cuál de los dibujos hay ángulos opuestos por el vértice?
Solución Paso a Paso
Recuerda la definición de ángulos opuestos por el vértice:
Los ángulos opuestos por el vértice son ángulos cuya formación es posible cuando dos rectas se cruzan, y se forman en el punto de intersección, una enfrentada a la otra. Los ángulos agudos son iguales en tamaño.
El dibujo de la respuesta A corresponde a esta definición.
Respuesta
Ejercicio #3
es paralela a
Determina cuál de las afirmaciones es correcta.
Solución en video
Solución Paso a Paso
Recuerda la definición de ángulos adyacentes:
Los ángulos adyacentes son ángulos cuya formación es posible en una situación en la que hay dos líneas rectas que se cruzan. Estos ángulos se forman en el punto donde se produce la intersección, uno contiguo al otro, y de aquí también sale su nombre.
Recuerda la definición de ángulos colaterales:
Dos ángulos formados cuando dos o más líneas paralelas son cortadas por una tercera línea. Los ángulos colaterales están del mismo lado de la línea de corte e incluso están a diferente altura en relación con la línea paralela a la que son adyacentes.
Por lo tanto, la respuesta C es correcta para esta definición.
Respuesta
Colaterales Adyacentes
Ejercicio #4
Las rectas en el dibujo son paralelas entre sí.
¿Qué ángulos se describen en la figura?
Solución Paso a Paso
Recordemos que los ángulos alternos se pueden definir como un par de ángulos que se pueden encontrar en el aspecto opuesto de una recta trazada para cortar dos líneas paralelas entre sí.
Además, estos ángulos se ubican en el nivel opuesto con respecto a la recta correspondiente a la que pertenecen.
Respuesta
Alternos
Ejercicio #5
¿Qué ángulos están marcados con la letra A en el dibujo?
¿Y cuáles con la letra B?
Responda la pregunta asumiendo que ABCD es un rectángulo
Solución Paso a Paso
Recordemos la definición de ángulos correspondientes:
Los ángulos correspondientes son ángulos situados en el mismo lado de la recta que corta a las dos paralelas y también están situados en el mismo nivel con respecto a la recta paralela a la que son adyacentes.
Parece que según esta definición estos son los ángulos marcados con la letra A.
Recordemos la definición de ángulos adyacentes:
Los ángulos adyacentes son ángulos cuya formación es posible en una situación en la que hay dos rectas que se cruzan.
Estos ángulos se forman en el punto donde se produce la intersección, uno al lado del otro, y de aquí también proviene su nombre.
Los ángulos adyacentes siempre se complementan en ciento ochenta grados, es decir, su suma es 180 grados.
Parece que según esta definición estos son los ángulos marcados con la letra B.
Respuesta
A- correspondientes B- adyacentes
- Líneas paralelas (Rectas paralelas)
- Altura del triángulo
- Rectas perpendiculares
- Deltoide
- Área del deltoide:
- Lados, vértices, y ángulos
- Notación de ángulos
- Bisectriz
- Tipos de ángulos
- Ángulo recto
- Ángulo agudo
- Ángulo obtuso
- Ángulo plano
- Suma y diferencia de ángulos
- Suma de los ángulos de un polígono
- Suma de los ángulos internos de un triángulo
- Los lados o aristas de un triángulo
- Paralelogramo
- El área del paralelogramo: ¿qué es y cómo se calcula?
- Perímetro de un paralelogramo
- Trapecios
- Área de un trapecio
- Perímetro de un trapecio
- Rectángulo
- ¿Cómo se calcula el área de un rectángulo?
- El perímetro del rectángulo
- Rectángulos congruentes
- Ángulo exterior de un triángulo
- Área
- Perímetro
- Triángulo
- Tipos de triángulos
- Triángulo obtuso
- Triángulo equilátero
- Identificación de un triángulo isósceles
- Triángulo escaleno
- Triángulo agudo
- Triángulo isósceles
- Área de un triángulo
- Área de un triángulo rectángulo
- Área del triángulo isósceles
- Área del triángulo escaleno
- Área del triángulo equilátero
- Perímetro de un triángulo
- Áreas de Polígonos para 7º Grado
- Triángulo Rectángulo
- Área de un trapecio rectángulo
- Área de un trapecio isósceles
- Mediana en un triángulo
- Centro de un Triángulo - El Centroide - El Punto de Intersección de las Medianas
- ¿Cómo calculamos el área de figuras complejas?
- ¿Cómo calculamos el perímetro de los polígonos?
- Todos los términos en el cálculo de triángulos
- ¿Cómo calcular el área de un triángulo usando trigonometría?
- Orden de operaciones básicas: suma, resta, multiplicación y división
- Orden de las operaciones básicas (potencias)
- Orden de operaciones básicas: raíces
- El 0 y el 1 en el orden de las operaciones
- Inverso multiplicativo
- Orden de las operaciones: paréntesis
- La propiedad conmutativa
- La propiedad asociativa
- Cómo calcular el área de un ortoedro
- Potenciación de números enteros
- Las Tablas de Multiplicar
- Fracciones









