Cuando los estudiantes escuchan las palabras "figuras compuestas", generalmente se sienten incómodos. Justo antes de que también te preguntes: "Oh, ¿por qué esto otra vez?", debes saber que no hay una razón real. Describir las figuras como compuestas no las hace realmente así. Resulta que calcular áreas y perímetros de figuras compuestas es en realidad relativamente sencillo.
Área de Rectángulos y Figuras Compuestas - Práctica
Domina el cálculo del área de rectángulos y figuras complejas con ejercicios paso a paso. Aprende a dividir formas compuestas en rectángulos familiares.
- Calcula el área de rectángulos usando la fórmula largo × ancho
- Identifica rectángulos ocultos dentro de figuras complejas
- Divide figuras compuestas en formas familiares más simples
- Suma y resta áreas de rectángulos para resolver figuras complejas
- Aplica propiedades del rectángulo para completar medidas faltantes
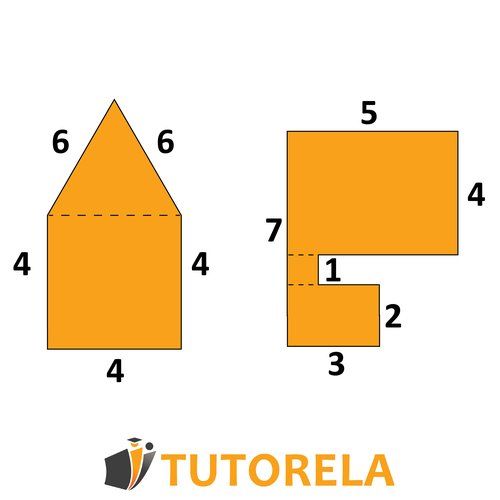
- Resuelve problemas reales con figuras compuestas en forma de L
Entendiendo la Área del rectángulo
¿Cómo calculamos el área de figuras complejas?
Serás introducido a las figuras complejas solo después de que aprendas varias figuras en geometría. La razón por la que estas figuras son complejas se debe al hecho de que son ligeramente diferentes de las que has llegado a conocer. En cada figura compleja, hay figuras adicionales ocultas que necesitas identificar. Dividir la figura compleja en varias figuras diferentes (y familiares) te permitirá responder a la pregunta de cómo calcular el área de figuras complejas.
El truco: extraer una forma familiar dentro de la forma compleja
Entonces, ¿cómo respondemos a la pregunta de cómo calcular el área de figuras complejas? Primero, necesitas identificar figuras familiares dentro de la figura compleja. Un ejemplo de esto: un rectángulo. Como sabes, cada figura tiene propiedades que conoces, así que dentro de la figura compleja, puedes aplicar las propiedades de la figura familiar y así calcular áreas y perímetros.
Después de completar los datos faltantes (según las propiedades de cada figura, por ejemplo: rectángulo), puedes completar el "rompecabezas", identificar datos adicionales que se te revelan y así calcular el área de la figura compleja. Al calcular el área de figuras complejas, a menudo necesitarás realizar operaciones aritméticas simples como división y suma (principalmente para los lados de la figura) - todo basado en las propiedades únicas de cada figura.
Practicar Área del rectángulo
Dado el siguiente rectángulo:
Halla el área del rectángulo.
ejemplos con soluciones para Área del rectángulo
Calcula el área del paralelogramo según los datos.
Como sabemos que ABCD es un paralelogramo, según las propiedades del mismo todo par de lados opuestos son iguales y paralelos.
Por lo tanto
Calculamos el área del paralelogramo según la fórmula de lado por la altura que desciende de ese lado, por lo tanto el área del paralelogramo es igual a:
Respuesta:
70
Calcula el área del triángulo siguiente:
La fórmula de cálculo del área triangular es:
(el lado * la altura del lado que desciende al lado) /2
Es decir:
Ahora reemplazamos los datos existentes:
Respuesta:
10
Dado el siguiente rectángulo:
Halla el área del rectángulo.
Calculemos el área del rectángulo multiplicando el largo por el ancho:
Respuesta:
10
Dado el trapecio:
¿Cuál es el área?
Fórmula del área de un trapecio:
Reemplazamos los datos en la fórmula y resolvemos:
Respuesta:
52.5
El ancho del rectángulo es igual a 15 cm y el largo es igual a 3 cm
Calcula el área del rectángulo
Para calcular el área del rectángulo, multiplicamos el largo por el ancho:
Respuesta:
45