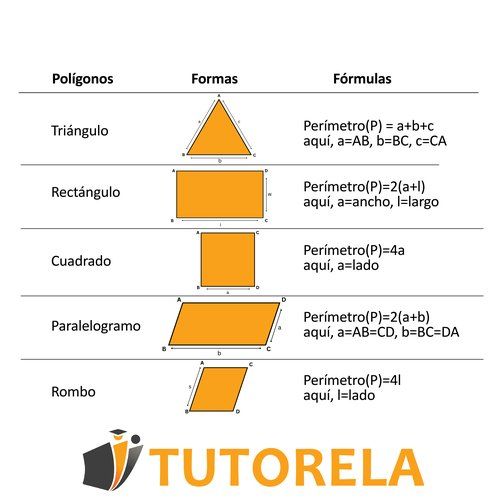
Mientras estemos tratando con una figura caracterizada por líneas rectas, el cálculo del perímetro se realizará sumando todas las longitudes de los lados. Esta es una operación aritmética simple que no requiere ninguna habilidad especial. Por ejemplo:
Perímetro del triángulo - Ejemplos, Ejercicios y Soluciones
Entendiendo la Perímetro del triángulo
Explicación completa con ejemplos
¿Cómo calculamos el perímetro de los polígonos?
El perímetro de una figura con lados de 5, 9, 4, 6 y 7, será 31. Todo lo que necesitas hacer es simplemente sumar todos los lados.
¿Por qué puede ser desafiante una pregunta así? Debido a que en los exámenes, no quieren evaluarte en operaciones aritméticas como la suma, sino en tu dominio de las propiedades de figuras específicas. Por lo tanto, necesitas conocer las propiedades de los polígonos tal como son.
Practicar Perímetro del triángulo
Pon a prueba tus conocimientos con más de 53 cuestionarios
Dado el trapecio de la figura
Dado que la base larga es mayor por 1.5 que la corta
Halla el perímetro del trapecio
ejemplos con soluciones para Perímetro del triángulo
Soluciones paso a paso incluidas
Ejercicio #1
Dado el rectángulo que tiene un lado AB de largo 4.8 cm y el lado AD de largo 12 cm.
¿Cuál es el perímetro del rectángulo?
Solución Paso a Paso
En el dibujo tenemos un rectángulo, aunque no está colocado en su forma estándar y está ligeramente girado,
pero esto no afecta que sea un rectángulo, y todavía tiene todas las propiedades de un rectángulo.
El perímetro de un rectángulo es la suma de todos sus lados, es decir, para hallar el perímetro del rectángulo tendremos que sumar las longitudes de todos los lados.
También sabemos que en un rectángulo los lados opuestos son iguales.
Por lo tanto, podemos usar los lados existentes para completar las longitudes que faltan.
4.8+4.8+12+12 =
33.6 cm
Respuesta:
33.6 cm
Solución en video
Ejercicio #2
Dado el triángulo:
¿Cuál es el perímetro del triángulo?
Solución Paso a Paso
El perímetro del triángulo es igual a la suma de todos los lados juntos, por lo tanto:
Respuesta:
24
Solución en video
Ejercicio #3
Dado el triángulo:
¿Cuál es su perímetro?
Solución Paso a Paso
El perímetro de un triángulo es igual a la suma de todos los lados juntos:
Respuesta:
31
Solución en video
Ejercicio #4
Dado el trapecio de la figura, ¿cuál es su perímetro?
Solución Paso a Paso
Para hallar el perímetro sumaremos todos los lados:
Respuesta:
24
Solución en video
Ejercicio #5
Dado el paralelogramo:
Calcule el perímetro del paralelogramo.
Solución Paso a Paso
Como en un paralelogramo todo par de lados opuestos son iguales:
El perímetro del paralelogramo es igual a la suma de todos los lados juntos:
Respuesta:
20
Solución en video