Ejercicios de Perímetro del Triángulo - Práctica Online

Domina el cálculo del perímetro del triángulo con ejercicios paso a paso. Aprende fórmulas para triángulos equiláteros, isósceles y escalenos.

📚¿Qué aprenderás con estos ejercicios de perímetro del triángulo?
  • Calcular el perímetro sumando los tres lados de cualquier triángulo
  • Aplicar la fórmula P = 3a para triángulos equiláteros
  • Resolver problemas con triángulos isósceles usando dos lados iguales
  • Identificar las unidades de medida correctas en cm, mm y metros
  • Convertir entre diferentes unidades de longitud según el problema
  • Resolver ejercicios con figuras compuestas que incluyen triángulos

Entendiendo la Perímetro

Explicación completa con ejemplos

¿Qué es el perímetro?

El perímetro indica la distancia que andaremos si salimos de determinado punto, completamos una vuelta completa y volvemos exactamente al punto de salida.
Por ejemplo, si nos preguntan cuál es el perímetro de la cintura, tomaremos un metro y mediremos el perímetro desde un cierto punto hasta completar una vuelta entera y llegar de regreso al mismo punto del cual comenzamos la medición.
Exactamente así también funciona en matemáticas. El perímetro de cualquier figura es la distancia desde un punto específico hasta volver a él después de haberla rodeado completamente.
Si esta es nuestra figura:

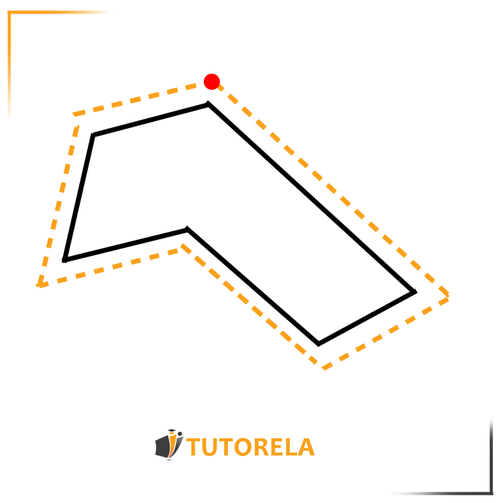
Qué es el perímetro

Su perímetro será la distancia que pasaremos si transitamos sobre su línea desde un cierto punto, y volvemos a él después de dar una vuelta completa. Imagina que rodeas la figura:

Explicación completa

Practicar Perímetro

Pon a prueba tus conocimientos con más de 80 cuestionarios

Dado un triángulo equilátero:

555

¿Cuál es su perímetro?

ejemplos con soluciones para Perímetro

Soluciones paso a paso incluidas
Ejercicio #1

Halla el perímetro del paralelogramo ABCD

Es sabido que CD es paralela a AB

777121212AAABBBCCCDDD

Solución Paso a Paso

Recordemos las propiedades del paralelogramo, en el que los pares de lados opuestos son paralelos e iguales.

Por lo tanto, AB es paralela a CD

Por lo tanto, BC es paralela a AD

De aquí se deduce que AB=CD=7

Además BC=AD=12

Ahora podemos calcular el perímetro, sumando todos los lados:

7+7+12+12=14+24=38 7+7+12+12=14+24=38

Respuesta:

38

Solución en video
Ejercicio #2

Dado el triángulo:

777111111131313

¿Cuál es su perímetro?

Solución Paso a Paso

El perímetro de un triángulo es igual a la suma de todos los lados juntos:

11+7+13=11+20=31 11+7+13=11+20=31

Respuesta:

31

Solución en video
Ejercicio #3

Dado el círculo de la figura,
su centro es el punto O

888OOO ¿Cuál es la circunferencia?

Solución Paso a Paso

Utilizamos la fórmula:P=2πr P=2\pi r

Reemplazamos los datos en la fórmula:P=2×8π P=2\times8\pi

P=16π P=16\pi

Respuesta:

16π 16\pi cm

Solución en video
Ejercicio #4

Dado el trapecio de la figura, ¿cuál es su perímetro?

444555999666

Solución Paso a Paso

Para hallar el perímetro sumaremos todos los lados:

4+5+9+6=9+9+6=18+6=24 4+5+9+6=9+9+6=18+6=24

Respuesta:

24

Solución en video
Ejercicio #5

Dado el paralelogramo:

666444AAABBBDDDCCC

Calcule el perímetro del paralelogramo.

Solución Paso a Paso

Como en un paralelogramo todo par de lados opuestos son iguales:

AB=CD=6,AC=BD=4 AB=CD=6,AC=BD=4

El perímetro del paralelogramo es igual a la suma de todos los lados juntos:

4+4+6+6=8+12=20 4+4+6+6=8+12=20

Respuesta:

20

Solución en video

Preguntas Frecuentes

Todo lo que necesitas saber Perímetro

¿Cómo se calcula el perímetro de un triángulo?

+
El perímetro de un triángulo se calcula sumando las longitudes de sus tres lados. La fórmula general es P = a + b + c, donde a, b y c son las medidas de cada lado del triángulo.

¿Cuál es la fórmula del perímetro de un triángulo equilátero?

+
Para un triángulo equilátero, donde todos los lados son iguales, la fórmula es P = 3a, donde 'a' representa la longitud de cualquier lado. Solo necesitas conocer la medida de un lado para calcular el perímetro completo.

¿Cómo calcular el perímetro de un triángulo isósceles?

+
En un triángulo isósceles tienes dos lados iguales y una base diferente. La fórmula es P = 2a + b, donde 'a' es la longitud de los lados iguales y 'b' es la longitud de la base.

¿En qué unidades se mide el perímetro del triángulo?

+
El perímetro se mide en unidades de longitud como: • Milímetros (mm) • Centímetros (cm) • Metros (m) Recuerda que 1 cm = 10 mm y 1 metro = 100 cm para hacer conversiones.

¿Qué datos necesito para calcular el perímetro de un triángulo?

+
Necesitas conocer la longitud de los tres lados del triángulo. En casos especiales: para un triángulo equilátero solo necesitas un lado, para un isósceles necesitas un lado igual y la base.

¿Cuál es la diferencia entre perímetro y área del triángulo?

+
El perímetro es la suma de todos los lados del triángulo (se mide en unidades lineales como cm). El área es la superficie interior del triángulo (se mide en unidades cuadradas como cm²). Son conceptos completamente diferentes.

¿Cómo resolver ejercicios de perímetro con triángulos en figuras compuestas?

+
En figuras compuestas: 1. Identifica todos los lados del triángulo que forman el contorno exterior 2. No olvides ningún lado en tu recorrido 3. Suma únicamente los lados que forman el perímetro total de la figura

¿Qué errores comunes se cometen al calcular el perímetro del triángulo?

+
Los errores más frecuentes son: olvidar sumar uno de los tres lados, confundir perímetro con área, usar unidades de medida incorrectas, y en figuras compuestas, contar lados internos que no forman parte del contorno exterior.

Continúa tu viaje matemático

Domina primero la Perímetro, luego avanza a estos temas relacionados que construyen sobre tus habilidades con fracciones

Temas sugeridos para practicar con anticipación

Altura del triánguloSuma de los ángulos internos de un triánguloLos lados o aristas de un triánguloÁngulo exterior de un triánguloÁreaTriánguloTipos de triángulosTriángulo obtusoTriángulo equiláteroIdentificación de un triángulo isóscelesTriángulo escalenoTriángulo agudoTriángulo isóscelesÁrea de un triánguloÁrea de un triángulo rectánguloÁrea del triángulo isóscelesÁrea del triángulo escalenoÁrea del triángulo equiláteroÁreas de Polígonos para 7º GradoTriángulo RectánguloMediana en un triánguloCentro de un Triángulo - El Centroide - El Punto de Intersección de las Medianas¿Cómo calculamos el área de figuras complejas?Todos los términos en el cálculo de triángulos¿Cómo calcular el área de un triángulo usando trigonometría?

Temas que se aprenden en secciones posteriores

Perímetro de un triángulo¿Cómo calculamos el perímetro de los polígonos?

Practica por Tipo de Pregunta

Elige tu estilo de aprendizaje y formato de práctica preferido para problemas de fracciones
Aplicación de la fórmula Aumentando un elemento específico por adición de..... o multiplicación por....... Calcular el lado faltante basado en la fórmula Cálculo de las partes del círculo Encontrar el área de la base en el perímetro y viceversa Identificando y definiendo elementos Identificar el valor mayor Problemas escritos Resta o suma a una forma más grande Una forma que consiste en varias formas (requiriendo la misma fórmula) Usando formas geométricas adicionales Uso del Teorema de Pitágoras Uso de variables Verificar si la fórmula es aplicable o no Aplicación de la fórmula Calcular el lado faltante basado en la fórmula Encontrar el área de la base en el perímetro y viceversa Usando formas geométricas adicionales Usando las propiedades del perímetro del paralelogramo Uso de variables Aplicación de la fórmula Ejercicios de comprensión Encontrar el área de la base en el perímetro y viceversa Uso de congruencia y semejanza Uso del Teorema de Pitágoras Uso de variables Aplicación de la fórmula Calcular el lado faltante basado en la fórmula Comparación entre 2 de la misma forma con un perímetro idéntico Encontrar el área de la base en el perímetro y viceversa Uso de variables Aplicación de la fórmula El perímetro de un triángulo Encontrar el área de la base en el perímetro y viceversa