Hasta ahora hemos trabajado con figuras bidimensionales comunes como, por ejemplo, el cuadrado o el triángulo.
Las figuras tridimensionales son aquellas que se extienden a la tercera dimensión, es decir, que además de longitud y anchura también tienen altura (o sea, la figura tiene profundidad).
Ejercicios de Ortoedros y Figuras Tridimensionales
Practica el cálculo de volumen, área superficial y propiedades de ortoedros, cilindros y prismas triangulares con ejercicios paso a paso
📚Domina las Figuras Tridimensionales con Ejercicios Prácticos
- Calcula el volumen de ortoedros usando largo × ancho × altura
- Determina el área superficial de cilindros con la fórmula 2πR×H+2π×R²
- Identifica caras, bordes y vértices en figuras tridimensionales
- Resuelve problemas de área lateral de ortoedros y prismas
- Aplica la fórmula V=π×R²×H para encontrar volúmenes de cilindros
- Diferencia entre diagonales de cara y diagonales del ortoedro
Entendiendo la Ortoedro
Explicación completa con ejemplos
Figuras tridimensionales
¿Qué son las figuras tridimensionales?
¿Qué diferencia tienen las figuras tridimensionales?
Las figuras tridimensionales cuentan con varias definiciones que enseguida veremos:
A continuación hay una figura tridimensional que usaremos para aprender cada definición - El cubo:
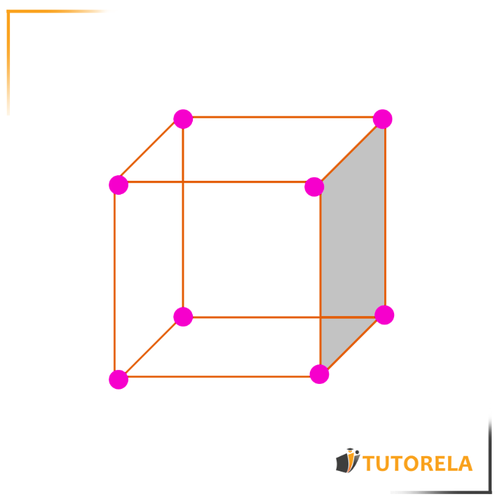
Cara: es el lado plano de una figura tridimensional
En el cubo que tenemos aquí hay 6 caras (una de ellas está pintada de color gris)
Borde: son las aristas que unen una cara con la otra en una figura tridimensional
En el cubo que tenemos aquí hay 12 bordes (pintados de verde)
Vértice: es el punto que une los bordes
En el cubo que tenemos aquí hay 8 vértices (pintados de anaranjado)
Volumen: es la cantidad de espacio contenido dentro de una figura tridimensional.
Las unidades de medida son .
Practicar Ortoedro
Pon a prueba tus conocimientos con más de 25 cuestionarios
Dado el ortoedro:
¿Cuál es el volumen del ortoedro?
ejemplos con soluciones para Ortoedro
Soluciones paso a paso incluidas
Ejercicio #1
Dado un ortoedro cuyas dimensiones en el dibujo
¿Qué rectángulos forman el ortoedro?
Solución Paso a Paso
Cada ortoedro, en realidad, esta compuesto de rectángulos, estos rectángulos son las caras del ortoedro.
Como sabemos que en un rectángulo las caras paralelas son iguales entre sí, podemos concluir que por cada cara encontrada habrá dos rectángulos.
Veamos primero la cara pintada de naranja,
Tiene ancho y alto, 5 y 3, entonces ya sabemos que son dos rectángulos de tamaño 5x6
Ahora veamos las caras de lado, también tienen una altura de 3, pero su ancho es de 6,
Y luego entendemos que hay dos rectángulos más de 3x6
Ahora veamos las caras superior e inferior, vemos que sus dimensiones son 5 y 6,
Por lo tanto, hay dos rectángulos más que tienen un tamaño de 5x6
Es decir, hay
2 rectángulos 5X6
2 rectángulos 3X5
2 rectángulos 6X3
Respuesta:
2 Rectángulos 5X6
2 Rectángulos 3X5
2 Rectángulos 6X3
Solución en video
Ejercicio #2
Dado el siguiente ortoedro
¿Cuál es la superficie?
Solución Paso a Paso
Identificamos que las caras son
3*3, 3*11, 11*3
Como las caras opuestas de un ortoedro son iguales, sabemos que por cada cara que encontramos hay otra cara, por lo tanto:
3*3, 3*11, 11*3
o
(3*3, 3*11, 11*3 ) *2
Para hallar el área de la superficie, tendremos que sumar todas estas áreas, por lo tanto:
(3*3+3*11+11*3 )*2
¡Y esta es en realidad la fórmula para el área de superficie!
Calculamos:
(9+33+33)*2
(75)*2
150
Respuesta:
150
Solución en video
Ejercicio #3
Dado el ortoedro cuyo largo es igual a 7 cm
El ancho es igual a 3 cm
La altura del ortoedro es igual a 5 cm
Calcule el volumen del cubo
Solución Paso a Paso
La fórmula para calcular el volumen de una ortoedro es:
altura*largo*ancho
Reemplazamos los datos en la fórmula:
3*5*7
7*5 = 35
35*3 = 105
Respuesta:
105 cm³
Solución en video
Ejercicio #4
Dado el despliegue del ortoedro
¿Cuál es la superficie del ortoedro?
Solución Paso a Paso
Para calcular la superficie del ortoedro, necesitaremos identificar sus tres caras (cada cara aparece dos veces):
1*3
1*8
3*8
La fórmula de la superficie de un ortoedro es la suma de todas las áreas de las caras, es decir:
Reemplazamos los datos en la fórmula:
2*(1*3+1*8+3*8)=
2*(3+8+24) =
2*35 =
70
¡Y esta es la solución!
Respuesta:
70
Solución en video
Ejercicio #5
Dado el siguiente ortoedro
¿Cuál es la superficie?
Solución Paso a Paso
Primero, recordamos la fórmula para el área de superficie del ortoedro:
(ancho*largo + altura*ancho + altura*largo) *2
Como en el ortoedro, las caras opuestas son iguales entre sí, los datos existentes son suficientes para llegar a una solución.
Reemplazamos los datos en la fórmula:
(8*5+3*5+8*3) *2 =
(24+40+15) *2 =
79*2 =
158
Respuesta:
158
Solución en video
Preguntas Frecuentes
¿Cómo calcular el volumen de un ortoedro paso a paso?
+Para calcular el volumen de un ortoedro multiplica: largo × ancho × altura. Por ejemplo, si un ortoedro mide 5cm × 3cm × 2cm, su volumen será 5 × 3 × 2 = 30 cm³. Las unidades siempre serán cúbicas (cm³, m³, etc.).
¿Cuál es la diferencia entre área superficial y área lateral?
+El área superficial incluye todas las caras de la figura (bases + caras laterales), mientras que el área lateral solo considera las caras laterales sin las bases. En un ortoedro, el área lateral se calcula como 2×(a×h + b×h) donde a=largo, b=ancho, h=altura.
¿Cuántas caras, bordes y vértices tiene un ortoedro?
+Un ortoedro tiene: • 6 caras (rectángulos) • 12 bordes (aristas) • 8 vértices (esquinas). Estas características son las mismas para cualquier ortoedro, sin importar sus dimensiones.
¿Cómo se calcula el volumen de un cilindro?
+El volumen del cilindro se calcula con V = π × R² × H, donde R es el radio de la base y H es la altura. Si el radio es 3cm y la altura 5cm: V = 3.14 × 3² × 5 = 3.14 × 9 × 5 = 141.3 cm³.
¿Qué es una diagonal del ortoedro y cómo se diferencia de la diagonal de cara?
+La diagonal de cara conecta dos vértices de la misma cara rectangular. La diagonal del ortoedro conecta dos vértices opuestos que no están en la misma cara, atravesando todo el interior de la figura tridimensional.
¿Cómo calcular el área lateral de un cilindro?
+El área lateral del cilindro se calcula con S = 2πR × H, excluyendo las bases circulares. Para un cilindro con radio 4cm y altura 6cm: S = 2 × 3.14 × 4 × 6 = 150.72 cm².
¿Cuál es la fórmula del área superficial total de un ortoedro?
+La fórmula es: 2×(largo×ancho + largo×altura + ancho×altura). Se multiplica por 2 porque cada par de caras opuestas es idéntico. Por ejemplo: ortoedro de 4×3×2 cm tendrá área = 2×(4×3 + 4×2 + 3×2) = 2×(12+8+6) = 52 cm².
¿Qué diferencia hay entre un prisma triangular y un ortoedro?
+Un ortoedro tiene bases rectangulares y 6 caras rectangulares, mientras que un prisma triangular tiene bases triangulares y 3 caras rectangulares laterales. El ortoedro es un caso especial de prisma rectangular.