Triángulo

• Recta: Es la unión de una sucesión de puntos, que se ubican en forma lineal, es decir, no existen curvas entre ellos.
• Segmento: Es una porción de recta, que se unen entre dos puntos.
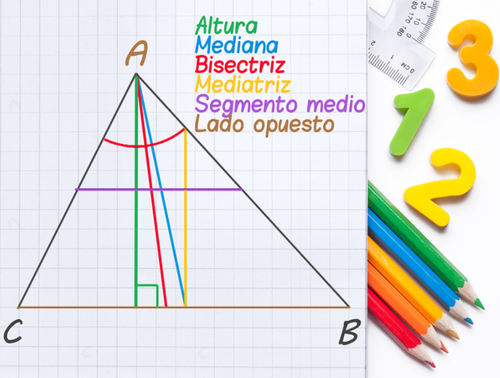
• Altura: La altura de un triángulo es la medida o longitud desde un vértice al punto más alto del triángulo, se suele denotar con la letra h.
• Mediana: la mediana es el segmento que se prolonga desde un vértice determinado hasta el punto medio del lado opuesto a dicho vértice.
• Bisectriz: la bisectriz es una semirrecta que se prolonga desde un vértice determinado, dividiéndolo en dos ángulos iguales.
• Mediatriz: la mediatriz es la línea que parte exactamente a la mitad sus lados y se puede trazar de forma perpendicular a dichos lados.
• Segmento medio: En el caso de los triángulos el segmento medio es aquella línea que podemos trazar ubicando los puntos medio de dos lados, esta línea medirá la mitad del tercer lado.
• Lado opuesto: un lado opuesto es aquel que se encuentra frente a un vértice determinado.

El triángulo es una figura compuesta por $3 º$ lados y la suma de todos sus ángulos siempre equivale a $180 º$.
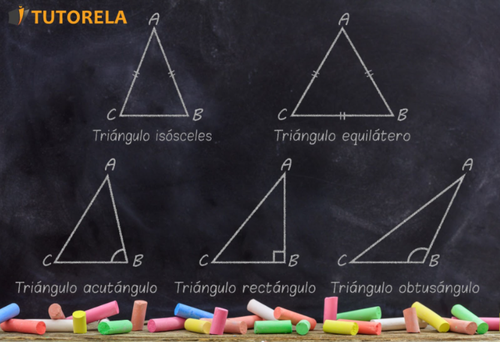
Hay varios tipos de triángulos:

Triángulo equilátero - Todos los lados (o aristas) son iguales, todos los ángulos son iguales y todas las alturas también son la mediana y la bisectriz.
Triángulo isósceles - Tiene dos lados iguales, dos ángulos base iguales y la mediana también es la altura y la bisectriz.
Triángulo rectángulo - Tiene un ángulo de $90 º$ grados formado por dos catetos. El lado opuesto al ángulo recto se denomina hipotenusa.
Triángulo escaleno - Todos los lados del triángulo son diferentes.

Pulsa aquí para una explicación más profunda acerca de los tipos de triángulos.

En todo triángulo, más allá del tipo de triángulo que sea, la suma de todos sus ángulos equivale a $180 º$.
En el triángulo equilátero -> cada ángulo vale $60 º$ grados.
En el triángulo isósceles -> los dos ángulos base son iguales y el tercero completa los $180 º$.
En el triángulo rectángulo -> sólo un ángulo vale $90 º$ y los otros dos completan los $180 º$.

Otra acotación:
En el triángulo especial de 90 º , 45 º , 45 º -> sólo un ángulo vale $90 º$ y los otros dos valen $45 º$ cada uno, esto concibe un triángulo que es un triángulo isósceles y rectángulo a la vez.

Ejercicio:
Dados los siguientes ángulos:
ángulo $A=80 º$
ángulo $B=50 º$
ángulo $C=50 º$

Pulsa aquí para una explicación más profunda sobre los ángulos de los triángulos.

Presentaremos aquí la fórmula general para calcular el área de los triángulos:

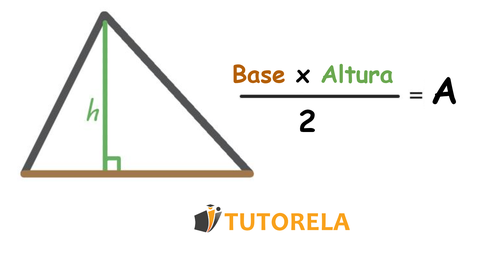
Esta fórmula sirve para calcular el área de los triángulos isósceles, equiláteros y escalenos.
Triángulo rectángulo

longitud del primer cateto $\times$ longitud del segundo cateto
\frac{longitud~del~primer~cateto~\times ~longitud~del~segundo~cateto

Pulsa aquí para una explicación más profunda sobre el área del triángulo.

El perímetro del triángulo equivale a la suma de las longitudes de todos los lados.

En un triángulo equilátero – todos los lados son iguales, por lo tanto, el perímetro del triángulo será 3\cdotlado
En un triángulo isósceles - hay dos lados iguales y conviene recordarlo cuando queremos deducir el perímetro

Pulsa aquí para una explicación más profunda sobre el perímetro del triángulo.

Los triángulos se consideran congruentes si todos sus ángulos y todos sus lados son iguales respectivamente.
Para demostrar que dos triángulos son congruentes deberás demostrar uno de los siguientes teoremas de congruencia:

ALA – ángulo, lado, ángulo
Si en ambos triángulos hay 2 ángulos iguales y la longitud del lado que comprenden también es igual, los triángulos son congruentes.

LAL – lado, ángulo, lado
Si en ambos triángulos hay 2 lados iguales y el ángulo adyacente también es igual, los triángulos son congruentes.

LLL - Lado, lado, lado
Si las longitudes de los 3 lados son iguales respectivamente en ambos triángulos, los triángulos son congruentes.

LLA - Lado, lado, ángulo
Si los 2 lados son iguales en ambos triángulos y también lo es el ángulo opuesto al lado más grande, los triángulos son congruentes.

Pulsa aquí para una explicación más profunda sobre la congruencia de triángulos.

Triángulos semejantes no deben tener áreas idénticas como ocurre con los triángulos congruentes, es suficiente que tengan las mismas proporciones.
Para demostrar que dos triángulos son semejantes deberás demostrar uno de los siguientes teoremas de semejanza:

AA – Ángulo, ángulo
Si dos de los ángulos de un triángulo son iguales a dos de los ángulos del otro, los triángulos son semejantes.

LLL - Lado, lado, lado
Si en un triángulo los tres lados son proporcionales a los tres lados del otro, los triángulos son semejantes.

Pulsa aquí para una explicación más profunda sobre la semejanza de triángulos.