Los intervalos de crecimiento y de decrecimiento describen las en las cuales la parábola sube y en aquellas en las que baja.
Veámoslo en una ilustración:
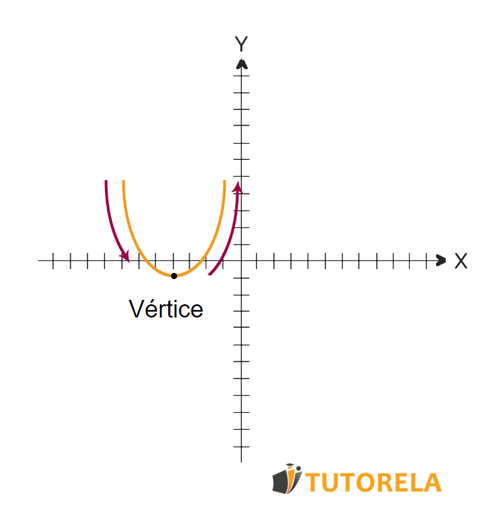
Siempre debemos observar la función de izquierda a derecha.
Cuando veamos una pendiente negativa (así se ve el decrecimiento) – la función es decreciente.
Cuando veamos una pendiente positiva (así se ve el crecimiento) – la función es creciente.
La parábola cambiará de intervalo sólo en un punto - en el vértice de la parábola.
De acuerdo con los datos en la gráfica
Encuentra el dominio donde la función es creciente
La gráfica de la función en el dibujo no intersecta el eje x
El vértice de la parábola es A
Elige el intervalo donde la función es decreciente
Respuesta:
x < A
La gráfica de la función interseca el eje x en los puntos A y B
El vértice de la parábola está marcado en el punto C
Elige el segmento donde la función es creciente
Respuesta:
x < C
La gráfica de la función interseca el eje x en los puntos A y B
El vértice de la parábola está marcado en el punto C
Elige el segmento donde la función es decreciente
Respuesta:
x > C
La gráfica de la función intersecta el eje x en los puntos A y B
El vértice de la parábola está marcado en el punto C
Elige el segmento donde la función aumenta
Respuesta:
x > C
La gráfica de la función interseca el eje x en los puntos A y B
El vértice de la parábola está marcado en el punto C
Elige el segmento donde la función es decreciente
Respuesta:
x < C