La parábola
Esta función es una función cuadrática y se denomina parábola.
Nos centraremos en dos tipos principales de parábolas: parábolas máximas y mínimas.
Practica ejercicios de función cuadrática: hallar vértice, puntos de intersección, áreas de crecimiento y dominios positivos/negativos con soluciones paso a paso.
Esta función es una función cuadrática y se denomina parábola.
Nos centraremos en dos tipos principales de parábolas: parábolas máximas y mínimas.
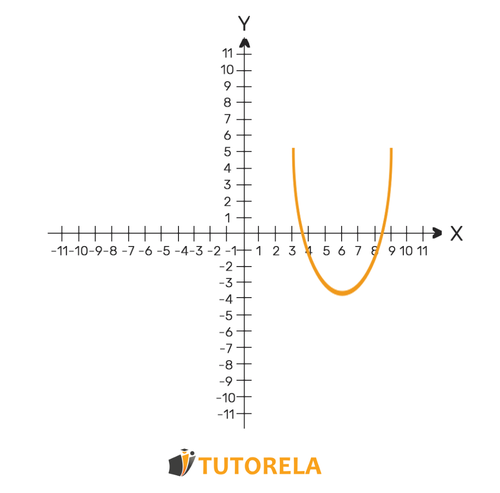
También llamada sonriente o feliz.
Un vértice es el punto mínimo de la función, donde es el más bajo.
Podemos identificar que es una parábola mínima si la ecuación es positiva.
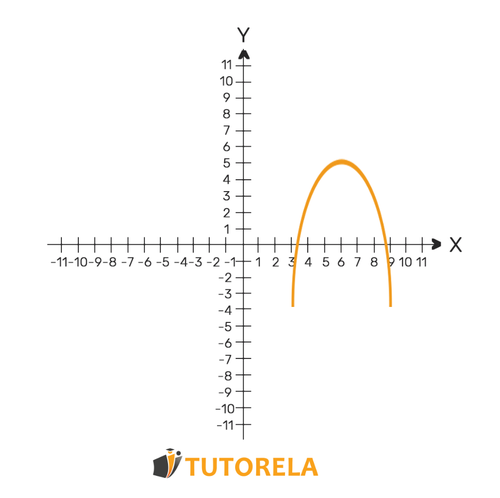
También llamado triste o llanto.
Un vértice es el punto máximo de la función, donde es el más alto.
Podemos identificar que es una parábola máxima si la ecuación es negativa.
A la parábola,
el vértice marca su punto más alto.
¿Cómo lo hallamos?
Identifica los coeficientes con base en la siguiente ecuación
\( y=x^2-6x+4 \)
¿Cuál es el valor del coeficiente en la ecuación?
La ecuación cuadrática del problema ya está ordenada (es decir, todos los términos de un lado y 0 del otro lado), por lo que nos acercamos a responder la pregunta formulada:
En el problema se hizo la pregunta: ¿cuál es el valor del coeficiente en la ecuación?
Recordemos las definiciones de los coeficientes al resolver una ecuación cuadrática y la fórmula de las raíces:
La regla dice que las raíces de una ecuación de la forma
es:
Es decir el coeficiente
es el término libre- es decir, el coeficiente del término elevado a la potencia cero -(Y esto se debe a que cualquier número distinto de cero elevado a la potencia cero es igual a 1:
)
Examinamos la ecuación del problema:
Tenga en cuenta que no hay ningún término libre en la ecuación, es decir, el valor numérico del término libre es 0, de hecho la ecuación se puede escribir de la siguiente manera:
y por lo tanto el valor del coeficiente es 0.
La respuesta correcta es la opción c.
Respuesta:
0
¿Cuál es el valor del coeficiente en la ecuación?
La ecuación cuadrática del problema ya está ordenada (es decir, todos los términos de un lado y 0 del otro lado), por lo que nos acercamos a responder la pregunta formulada:
En el problema se hizo la pregunta: ¿cuál es el valor del coeficiente en la ecuación?
Recordemos las definiciones de los coeficientes al resolver una ecuación cuadrática y la fórmula de las raíces:
La regla dice que las raíces de una ecuación de la forma
es :
Es decir, el coeficiente es el coeficiente del término en la primera potencia -. Examinamos la ecuación del problema:
Es decir, el número que multiplica a
es 8
entonces reconocemos a b, que es el coeficiente del término en la primera potencia, es el número,
La respuesta correcta es la opción d.
Respuesta:
8
De hecho, una ecuación cuadrática se compone así:
y = ax²-bx-c
Es decir,
a es el coeficiente de x², en este caso 2.
b es el coeficiente de x, en este caso 5.
Y c es el número sin incógnita al final, en este caso 6.
Respuesta:
Aquí tenemos una ecuación cuadrática.
Una ecuación cuadrática siempre se construye así:
Donde a, b y c generalmente ya los conocemos, y los puntos X e Y necesitan ser descubiertos.
En primer lugar, parece que en esta fórmula no tenemos la C,
Por lo tanto, entendemos que es igual a 0.
a es el coeficiente de X², aquí no tiene coeficiente, por lo tanto
es el número que viene antes de la X que no está al cuadrado.
Respuesta:
¿Cuál es el valor del coeficiente en la ecuación?
Respuesta:
-2