Ejercicios de Eje de Simetría en Parábolas - Práctica

Practica cómo encontrar el eje de simetría de parábolas usando la fórmula del vértice y puntos simétricos. Ejercicios resueltos paso a paso.

📚¿Qué aprenderás con estos ejercicios de simetría?
  • Aplicar la fórmula X = -b/2a para hallar el eje de simetría
  • Identificar el vértice de una parábola en funciones cuadráticas
  • Usar puntos simétricos para determinar el eje de simetría
  • Resolver problemas con funciones de la forma x² + bx + c
  • Verificar resultados usando diferentes métodos de cálculo
  • Interpretar gráficamente el concepto de simetría en parábolas

Entendiendo la Simetría

Explicación completa con ejemplos

El eje de simetría en una parábola es el eje que pasa por su vértice de tal modo que si plegáramos el lado derecho sobre el lado izquierdo, ambos lados se verían unidos.
Veámoslo en una ilustración:

Simetría 1

Para hallar el eje de simetría deberemos ubicar el valor de X X del vértice de la parábola o hacerlo a través de la fórmula del vértice de la parábola o con la ayuda de dos puntos simétricos sobre la parábola.

Fórmula del vértice de la parábola

X=−b2a X=\frac{-b}{2a}

Fórmula de dos puntos simétricos:

X Vértice

XVeˊrtice=El valor de X en el primer punto + El valor de X en el segundo punto2 X_{Vértice}=\frac{El~valor~de~X~en~el~primer~punto~+~El~valor~de~X~en~el~segundo~punto}{2}

Explicación completa

Practicar Simetría

Pon a prueba tus conocimientos con más de 4 cuestionarios

Dado la función cuadrática

\( f(x)=3x^2+6x-6 \)

Hallar el eje de simetría de la función

ejemplos con soluciones para Simetría

Soluciones paso a paso incluidas
Ejercicio #1

Dada la expresión de la función cuadrática

Se debe encontrar el eje simétrico de la expresión

f(x)=−3x2+3 f(x)=-3x^2+3

Solución Paso a Paso

Respuesta:

x=0 x=0

Solución en video
Ejercicio #2

Dada la expresión de la función cuadrática

Se debe encontrar el eje simétrico de la expresión

f(x)=7x2 f(x)=7x^2

Solución Paso a Paso

Respuesta:

x=0 x=0

Solución en video
Ejercicio #3

Dada la expresión de la función cuadrática

Encontrar el punto de simetría de la función

f(x)=2x2 f(x)=2x^2

Solución Paso a Paso

Respuesta:

(0,0) (0,0)

Solución en video
Ejercicio #4

Dada la expresión de la función cuadrática

Encontrar el punto de simetría de la función

f(x)=−5x2+10 f(x)=-5x^2+10

Solución Paso a Paso

Respuesta:

(0,10) (0,10)

Solución en video
Ejercicio #5

Dada la expresión de la función cuadrática

Encontrar el punto de simetría de la función

f(x)=12x2 f(x)=\frac{1}{2}x^2

Solución Paso a Paso

Respuesta:

(0,0) (0,0)

Solución en video

Preguntas Frecuentes

Todo lo que necesitas saber Simetría

¿Cómo se calcula el eje de simetría de una parábola?

+
Para calcular el eje de simetría de una parábola, usa la fórmula X = -b/2a, donde 'a' y 'b' son los coeficientes de la función cuadrática ax² + bx + c. También puedes usar dos puntos simétricos y promediar sus coordenadas X.

¿Qué es el eje de simetría en una parábola?

+
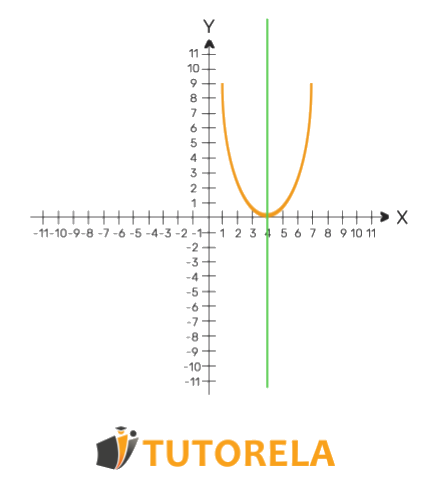
El eje de simetría es una línea vertical que pasa por el vértice de la parábola y la divide en dos partes iguales. Si doblaras la parábola por esta línea, ambos lados se superpondrían perfectamente.

¿Cuáles son los pasos para encontrar el eje de simetría con la fórmula del vértice?

+
Los pasos son: 1) Identifica los coeficientes a y b en la función cuadrática, 2) Sustituye en la fórmula X = -b/2a, 3) Realiza las operaciones matemáticas, 4) El resultado es la coordenada X del eje de simetría.

¿Cómo usar puntos simétricos para hallar el eje de simetría?

+
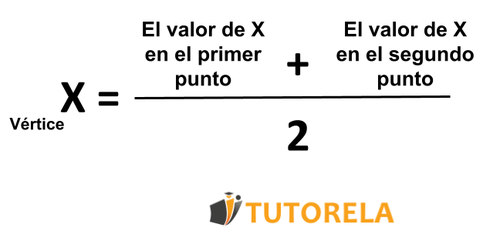
Si tienes dos puntos con la misma coordenada Y sobre la parábola, suma sus coordenadas X y divide entre 2. La fórmula es: X_vértice = (X₁ + X₂)/2, donde X₁ y X₂ son las coordenadas X de los puntos simétricos.

¿Por qué es importante conocer el eje de simetría de una parábola?

+
El eje de simetría te ayuda a: encontrar el vértice de la parábola, determinar el valor máximo o mínimo de la función, graficar la parábola con mayor precisión, y resolver problemas de optimización en matemáticas y física.

¿Qué errores comunes se cometen al calcular el eje de simetría?

+
Los errores más frecuentes incluyen: confundir los signos en la fórmula -b/2a, no identificar correctamente los coeficientes a y b, olvidar el signo negativo en la fórmula, y no verificar el resultado con puntos simétricos.

¿En qué tipo de funciones se puede aplicar el concepto de eje de simetría?

+
El eje de simetría se aplica principalmente en funciones cuadráticas de la forma f(x) = ax² + bx + c, donde a ≠ 0. También se encuentra en otras funciones parabólicas y en geometría con figuras simétricas como trapecios isósceles y rombos.

¿Cómo verificar si el eje de simetría calculado es correcto?

+
Puedes verificar el resultado de tres formas: 1) Sustituir puntos equidistantes del eje y comprobar que tienen el mismo valor Y, 2) Usar ambos métodos (fórmula del vértice y puntos simétricos) y comparar, 3) Graficar la función y verificar visualmente la simetría.

Continúa tu viaje matemático

Domina primero la Simetría, luego avanza a estos temas relacionados que construyen sobre tus habilidades con fracciones

Temas sugeridos para practicar con anticipación

La función cuadráticaParábolaConjuntos de positividad y negatividad de la función cuadráticaIntervalos de crecimiento y de decrecimiento de una parábolaVértice de la parábola

Practica por Tipo de Pregunta

Elige tu estilo de aprendizaje y formato de práctica preferido para problemas de fracciones
Eje de simetría Encontrando un punto estacionario