La representación gráfica de una función que representa una proporcionalidad directa es en realidad la capacidad de expresar una expresión algebraica mediante un gráfico. Como es una proporcionalidad directa, el gráfico será la de una línea recta.
La representación gráfica de una función que representa una proporcionalidad directa es en realidad la capacidad de expresar una expresión algebraica mediante un gráfico.
Como es una proporcionalidad directa directa, la gráfica será de una línea recta.
Una función que representa una proporcionalidad directa es una función lineal de la familia .
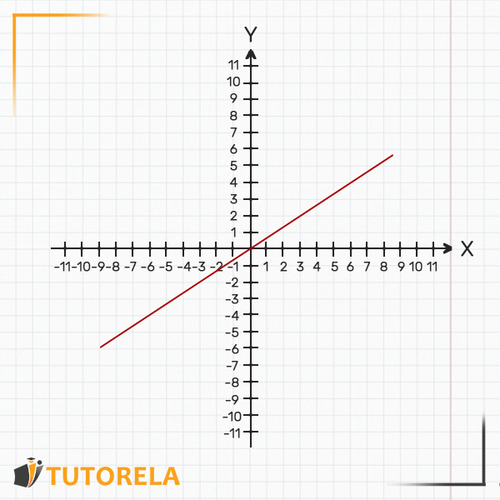
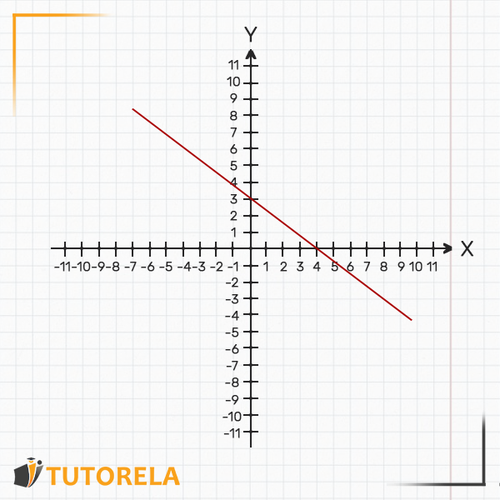
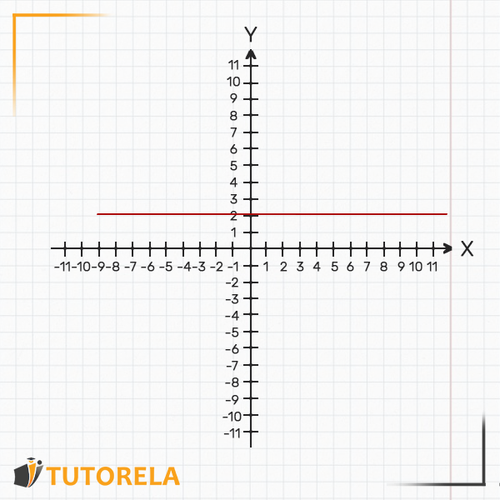
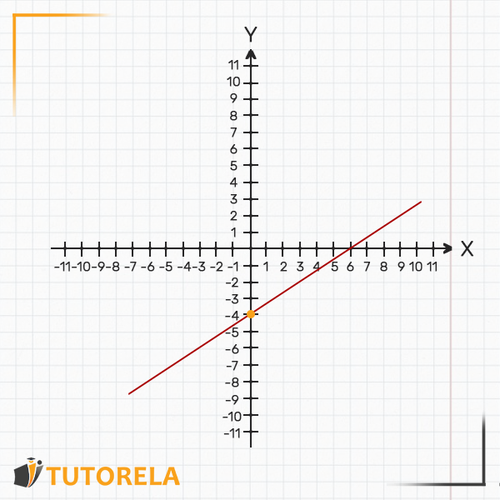
La representación gráfica de esta función es una línea recta ascendente, descendente o paralela al eje pero nunca paralela al eje .
Nota: observamos la línea de izquierda a derecha.
Ya podemos reconocer en la ecuación de la recta cómo es la representación gráfica de cada función:
(solo cuando la ecuación es explícita está aislado en un lado y su coeficiente es )