$$ \log_mn\times\log_zr= $$

$$ \log_{m\times z}(n\times r) $$

Ejercicios de Reglas de Logaritmos - Practica y Problemas

Domina las leyes logarítmicas con ejercicios paso a paso. Practica propiedades, cambio de base, logaritmo natural y resuelve problemas complejos.

📚¿Qué aprenderás practicando las reglas de logaritmos?

Aplicar las leyes fundamentales de logaritmos en ejercicios prácticos
Resolver ecuaciones logarítmicas usando propiedades de suma y resta
Dominar el cambio de base logarítmica para diferentes sistemas
Calcular logaritmos naturales y sus propiedades específicas
Simplificar expresiones complejas con múltiples logaritmos
Convertir entre forma logarítmica y exponencial correctamente

Entendiendo la Leyes de los logaritmos

Explicación completa con ejemplos

¿Qué son las leyes logarítmicas?

Hay algunas leyes logarítmicas que vale la pena conocer para facilitar la resolución de problemas. Las siguientes leyes son las reglas principales que utilizará. Cabe señalar que las letras a, m, n deben ser números reales y positivos para que estas leyes tengan validez.

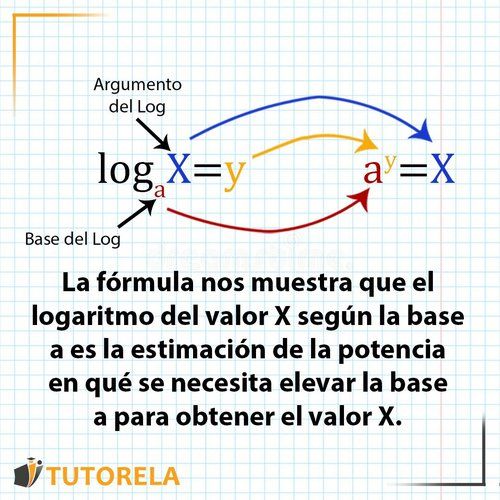
leyes logarítmicas

Valores constantes:

$log_a\left(1\right)=0$
$log_a\left(a\right)=1$

Operaciones aritméticas básicas

$log_aMN=log_aM+log_aN$
$log_aM/N=log_aM-log_aN$
$Log_a\left(M\right)\times Log_n\left(D\right)=Log_n\left(M\right)\times Log_a\left(D\right)$
$Log_aM^n=nLog_aM$

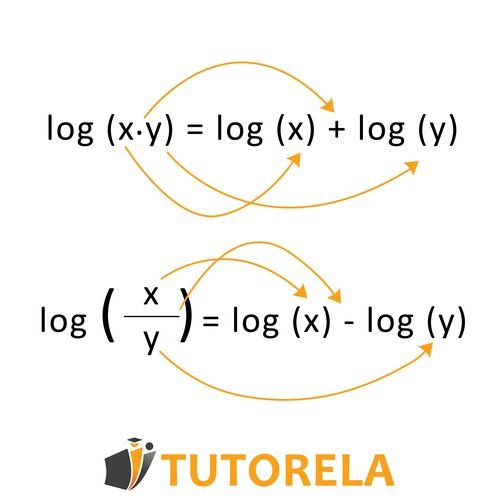
Explicación visual de las reglas de logaritmos que muestra que log(x·y) es igual a log(x) más log(y), y que log(x/y) es igual a log(x) menos log(y), con flechas para mayor claridad.

Cambiar la base del logaritmo:

$log_b\left(x\right)=log_c\left(x\right)/log_c\left(b\right)$
$log_b\left(c\right)=1/log_c\left(b\right)$

Fórmula de cambio de base logarítmica ilustrada: logaritmo base b de a es igual al logaritmo base x de a dividido por el logaritmo base x de b, con flechas que muestran la transformación.

Derivada del logaritmo:

$fx=log_b\left(x\right)⇒f^{\prime}x=1/xln(b)$

Integral del logaritmo:

$∫log_b\left(x\right)dx=x\times log_b\left(x\right)-1/ln\left(b\right)+C$

Explicación completa

Practicar Leyes de los logaritmos

Pon a prueba tus conocimientos con más de 38 cuestionarios

$\log_49\times\log_{13}7=$

ejemplos con soluciones para Leyes de los logaritmos

Soluciones paso a paso incluidas

Ejercicio #1

$2\log_82+\log_83=$

Solución Paso a Paso

$2\log_82=\log_82^2=\log_84$

$2\log_82+\log_83=\log_84+\log_83=$

$\log_84\cdot3=\log_812$

Respuesta:

$\log_812$

Solución en video

Ejercicio #2

$3\log_49+8\log_4\frac{1}{3}=$

Solución Paso a Paso

En donde:

$3\log_49=\log_49^3=\log_4729$

$8\log_4\frac{1}{3}=\log_4\left(\frac{1}{3}\right)^8=$

$\log_4\frac{1}{3^8}=\log_4\frac{1}{6561}$

Por lo tanto

$3\log_49+8\log_4\frac{1}{3}=$

$\log_4729+\log_4\frac{1}{6561}$

$\log_ax+\log_ay=\log_axy$

$\left(729\cdot\frac{1}{6561}\right)=\log_4\frac{1}{9}$

$\log_49^{-1}=-\log_49$

Respuesta:

$-\log_49$

Solución en video

Ejercicio #3

$\frac{1}{2}\log_24\times\log_38+\log_39\times\log_37=$

Solución Paso a Paso

Descomponemos en partes

$\log_24=x$

$2^x=4$

$x=2$

$\log_39=x$

$3^x=9$

$x=2$

Reemplazamos en la ecuación

$\frac{1}{2}\cdot2\log_38+2\log_37=$

$1\cdot\log_38+2\log_37=$

$\log_38+\log_37^2=$

$\log_38+\log_349=$

$\log_3\left(8\cdot49\right)=\log_3392$ $x=2$

Respuesta:

$\log_3392$

Solución en video

Ejercicio #4

$\frac{1}{4}\cdot\log_61296\cdot\log_6\frac{1}{2}-\log_63=$

Solución Paso a Paso

Descomponemos en partes

$\log_61296=x$

$6^x=1296$

$x=4$

$\frac{1}{4}\cdot4\cdot\log_6\frac{1}{2}-\log_63=$

$\log_6\frac{1}{2}-\log_63=$

$\log_6\left(\frac{1}{2}:3\right)=\log_6\frac{1}{6}$

$\log_6\frac{1}{6}=x$

$6^x=\frac{1}{6}$

$x=-1$

Respuesta:

$-1$

Solución en video

Ejercicio #5

$\log_7x^4-\log_72x^2=3$

?=x

Solución Paso a Paso

$\log_ax-\log_ay=\log_a\frac{x}{y}$

$\log_7x^4-\log_72x^2=$

$\log_7\frac{x^4}{2x^2}=3$

$7^3=\frac{x^2}{2}$

Multiplicamos por: $2$

$2\cdot7^3=x^2$

Extraemos la raíz

$x=\sqrt{680}=7\sqrt{14}$

$x=-\sqrt{680}=-7\sqrt{14}$

Respuesta:

$-7\sqrt{14\text{ }}\text{ , }7\sqrt{14}$

Solución en video

Preguntas Frecuentes

Todo lo que necesitas saber Leyes de los logaritmos

¿Cuáles son las principales leyes de logaritmos que debo memorizar?

Las leyes esenciales son: log_a(1) = 0, log_a(a) = 1, log_a(MN) = log_a(M) + log_a(N), log_a(M/N) = log_a(M) - log_a(N), y log_a(M^n) = n·log_a(M). Estas propiedades te permitirán resolver la mayoría de problemas logarítmicos.

¿Cómo resolver ecuaciones logarítmicas paso a paso?

1. Identifica el dominio de definición (argumentos > 0) 2. Aplica las leyes logarítmicas para simplificar 3. Convierte a forma exponencial cuando sea necesario 4. Resuelve la ecuación resultante 5. Verifica que las soluciones estén en el dominio

¿Cuándo usar el cambio de base en logaritmos?

Usa el cambio de base cuando necesites calcular logaritmos que no sean base 10 o e en tu calculadora. La fórmula es log_b(x) = log_c(x)/log_c(b), donde c puede ser 10 o e según tu calculadora.

¿Qué errores comunes debo evitar con logaritmos?

• No confundas log_a(M+N) con log_a(M) + log_a(N) - no son iguales • Recuerda que no existen logaritmos de números negativos o cero • Siempre verifica el dominio antes de resolver • No olvides que la base debe ser positiva y diferente de 1

¿Cuál es la diferencia entre logaritmo común y natural?

El logaritmo común tiene base 10 (log) y el natural tiene base e ≈ 2.718 (ln). Ambos siguen las mismas leyes, pero el logaritmo natural es especialmente útil en cálculo y aplicaciones científicas por sus propiedades únicas de derivación.

¿Cómo simplificar expresiones con múltiples logaritmos?

Usa las propiedades paso a paso: convierte productos en sumas, cocientes en restas, y potencias en multiplicaciones. Agrupa términos similares y busca oportunidades para aplicar log_a(a) = 1 o log_a(1) = 0.

¿Para qué sirven los logaritmos en la vida real?

Los logaritmos se usan en: escalas sísmicas (Richter), medición de sonido (decibeles), pH en química, crecimiento poblacional, interés compuesto, y algoritmos computacionales. Son fundamentales para modelar fenómenos exponenciales.

¿Cómo verificar si mi respuesta logarítmica es correcta?

Sustituye tu respuesta en la ecuación original y verifica que se cumpla la igualdad. También puedes convertir a forma exponencial: si log_a(x) = b, entonces a^b debe igual x. Siempre confirma que esté en el dominio válido.

Practica por Tipo de Pregunta

Elige tu estilo de aprendizaje y formato de práctica preferido para problemas de fracciones

Más Recursos y Enlaces

Explora más recursos y enlaces relacionados con Leyes de los logaritmos

Practicar Cambiando la Base de un Logaritmo Practicar Multiplicación de Logaritmos Practicar Cambio de Base de Logaritmo Practicar Suma de Logaritmos Practicar Resta de Logaritmos Practicar Potencia en logaritmo