$$ -3(\frac{\ln4}{\ln5}-\log_57+\frac{1}{\log_65})= $$

$$ \ln(\frac{5}{4})^3+\log_5(\frac{7}{6})^3 $$

Ejercicios de Resta de Logaritmos - Práctica con Soluciones

Domina la resta de logaritmos con misma base y bases diferentes. Ejercicios paso a paso, cambio de base y problemas resueltos para estudiantes.

📚¡Practica la Resta de Logaritmos!

Aplicar la regla log_a(x) - log_a(y) = log_a(x/y) con ejercicios prácticos
Resolver problemas de resta con logaritmos de base idéntica paso a paso
Dominar el cambio de base para restar logaritmos con bases diferentes
Identificar cuándo usar la fórmula log_a(X) = log_b(X)/log_b(a)
Resolver ecuaciones logarítmicas que involucran resta de logaritmos
Practicar con ejercicios desde básicos hasta avanzados con soluciones detalladas

Entendiendo la Resta de logaritmos

Explicación completa con ejemplos

Resta de Logaritmos

La definición de un logaritmo es:
$log_a⁡x=b$
$X=a^b$

Donde:
$a$ es la base del exponente
$X$ es lo que aparece dentro del logaritmo, también puede aparecer entre paréntesis
$b$ es el exponente al que elevamos la base del logaritmo para obtener el número que aparece dentro del logaritmo.

La resta de logaritmos con base idéntica se basa en la siguiente regla:

$log_a⁡x-log_a⁡y=log_a⁡\frac{x}{y}$

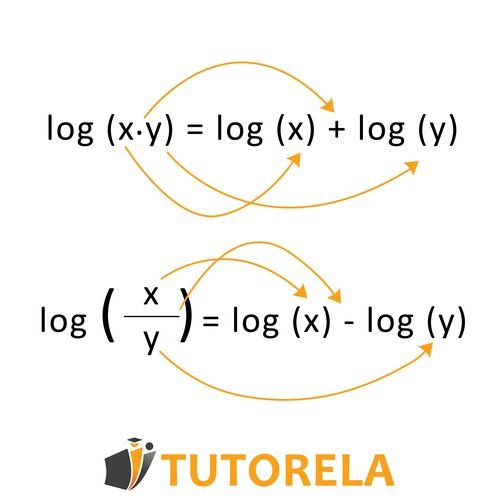
Explicación visual de las reglas logarítmicas que muestra que log(x·y) es igual a log(x) más log(y), y log(x/y) es igual a log(x) menos log(y), con flechas conectando cada parte para mayor claridad.

La resta de logaritmos con diferentes bases se realiza cambiando la base usando la siguiente regla:

$log_aX=\frac{log_{base~que~queremos~cambiar~a}X}{log_{base~que~queremos~cambiar~a}a}$

Fórmula de cambio de base logarítmica ilustrada: logaritmo base b de a es igual a logaritmo base x de a dividido por logaritmo base x de b, con flechas mostrando la transformación desde la forma original.

Explicación completa

Practicar Resta de logaritmos

Pon a prueba tus conocimientos con más de 6 cuestionarios

$x=\text{?}$

$\log_{\frac{1}{2}}5-\log_{\frac{1}{2}}4\le\log_{\frac{1}{2}}x-\log_{\frac{1}{2}}3$

ejemplos con soluciones para Resta de logaritmos

Soluciones paso a paso incluidas

Ejercicio #1

$\frac{1}{4}\cdot\log_61296\cdot\log_6\frac{1}{2}-\log_63=$

Solución Paso a Paso

Descomponemos en partes

$\log_61296=x$

$6^x=1296$

$x=4$

$\frac{1}{4}\cdot4\cdot\log_6\frac{1}{2}-\log_63=$

$\log_6\frac{1}{2}-\log_63=$

$\log_6\left(\frac{1}{2}:3\right)=\log_6\frac{1}{6}$

$\log_6\frac{1}{6}=x$

$6^x=\frac{1}{6}$

$x=-1$

Respuesta:

$-1$

Solución en video

Ejercicio #2

$\log_7x^4-\log_72x^2=3$

?=x

Solución Paso a Paso

$\log_ax-\log_ay=\log_a\frac{x}{y}$

$\log_7x^4-\log_72x^2=$

$\log_7\frac{x^4}{2x^2}=3$

$7^3=\frac{x^2}{2}$

Multiplicamos por: $2$

$2\cdot7^3=x^2$

Extraemos la raíz

$x=\sqrt{680}=7\sqrt{14}$

$x=-\sqrt{680}=-7\sqrt{14}$

Respuesta:

$-7\sqrt{14\text{ }}\text{ , }7\sqrt{14}$

Solución en video

Ejercicio #3

$\log7x+\log(x+1)-\log7=\log2x-\log x$

$?=x$

Solución Paso a Paso

Domino de definición

$x>0$

$x+1>0$

$x>-1$

$\log7x+\log\left(x+1\right)-\log7=\log2x-\log x$

$\log\frac{7x\cdot\left(x+1\right)}{7}=\log\frac{2x}{x}$

Reducimos por: $7$ y por $X$

$x\left(x+1\right)=2$

$x^2+x-2=0$

$\left(x+2\right)\left(x-1\right)=0$

$x+2=0$

$x=-2$

No dominio de definición $x>0$

$x-1=0$

$x=1$

Dominio de definición

Respuesta:

$1$

Solución en video

Ejercicio #4

$\log_29-\log_23=$

Solución Paso a Paso

Respuesta:

$\log_23$

Solución en video

Ejercicio #5

$\log_53-\log_52=$

Solución Paso a Paso

Respuesta:

$\log_51.5$

Solución en video

Preguntas Frecuentes

Todo lo que necesitas saber Resta de logaritmos

¿Cómo se resta logaritmos con la misma base?

Para restar logaritmos con la misma base, usa la regla: log_a(x) - log_a(y) = log_a(x/y). Esto significa que puedes convertir la resta en un solo logaritmo dividiendo los argumentos. Por ejemplo: log_7(147) - log_7(3) = log_7(147/3) = log_7(49) = 2.

¿Qué hacer cuando los logaritmos tienen bases diferentes?

Cuando las bases son diferentes, primero debes cambiar una o ambas bases para que sean iguales usando la fórmula de cambio de base: log_a(X) = log_b(X)/log_b(a). Después aplica la regla de resta normal. Es recomendable convertir a la base menor para simplificar los cálculos.

¿Cuál es la fórmula para cambio de base de logaritmos?

La fórmula de cambio de base es: log_a(X) = log_c(X)/log_c(a), donde 'c' es la nueva base deseada. En el numerador colocas el logaritmo con la nueva base y el mismo argumento original, en el denominador colocas el logaritmo de la base original con la nueva base.

¿Pueden restarse logaritmos de números negativos?

No, los logaritmos de números negativos no están definidos en los números reales. Los argumentos de los logaritmos (los números dentro del log) siempre deben ser positivos. Si aparece un número negativo en tu ejercicio, revisa el planteamiento del problema.

¿Cómo verifico si mi respuesta en resta de logaritmos es correcta?

Para verificar tu respuesta: 1) Sustituye el resultado en la ecuación original, 2) Convierte el logaritmo resultado a forma exponencial, 3) Verifica que la igualdad se cumple. Por ejemplo, si log_7(49) = 2, verifica que 7² = 49.

¿Qué errores comunes se cometen al restar logaritmos?

Los errores más comunes incluyen: 1) Intentar restar logaritmos con bases diferentes sin cambio de base, 2) Confundir el orden en la fracción (numerador y denominador), 3) Olvidar que log_a(x) - log_a(y) ≠ log_a(x-y), 4) No simplificar la fracción resultante antes de calcular el logaritmo final.

¿En qué situaciones se usa la resta de logaritmos en la vida real?

La resta de logaritmos se aplica en: cálculos de pH en química (diferencias de acidez), análisis de decibeles en acústica (comparación de intensidades sonoras), finanzas (cálculo de tasas de crecimiento relativas), y en estadística para comparar órdenes de magnitud entre datos.

¿Qué debo memorizar sobre las propiedades de logaritmos?

Debes memorizar estas reglas clave: 1) log_a(xy) = log_a(x) + log_a(y), 2) log_a(x/y) = log_a(x) - log_a(y), 3) log_a(x^n) = n·log_a(x), 4) log_a(1) = 0, 5) log_a(a) = 1, 6) La fórmula de cambio de base. Estas propiedades son fundamentales para resolver cualquier problema con logaritmos.

Continúa tu viaje matemático

Domina primero la Resta de logaritmos, luego avanza a estos temas relacionados que construyen sobre tus habilidades con fracciones

Temas sugeridos para practicar con anticipación

Suma de Logaritmos

Temas que se aprenden en secciones posteriores

Multiplicación de Logaritmos Potencia en logaritmo Cambiando la Base de un Logaritmo Cambio de Base de Logaritmo Logaritmos

Practica por Tipo de Pregunta

Elige tu estilo de aprendizaje y formato de práctica preferido para problemas de fracciones

Aplicación de la fórmula Desigualdad El resultado en una ecuación cuadrática Uso de múltiples reglas Uso de variables