Ejercicios de Suma de Logaritmos - Práctica Gratis Online

Practica la suma de logaritmos con la misma base y diferentes bases. Incluye cambio de base, propiedades logarítmicas y ejercicios resueltos paso a paso.

📚¿Qué aprenderás con estos ejercicios de suma de logaritmos?

Aplicar la regla log_a(x) + log_a(y) = log_a(x·y) para sumar logaritmos con misma base
Resolver ejercicios como log_8(32) + log_8(2) usando propiedades logarítmicas
Cambiar la base de logaritmos usando la fórmula log_a(x) = log_b(x)/log_b(a)
Sumar logaritmos con diferentes bases convirtiendo a una base común
Resolver ecuaciones logarítmicas complejas como log_25(x) + log_5(x) = 3
Identificar cuándo aplicar cada propiedad logarítmica según el tipo de problema

Entendiendo la Suma de logaritmos

Explicación completa con ejemplos

Suma de Logaritmos

La definición de un logaritmo es:

$log_a⁡x=b$
$X=a^b$

Donde:
$a$ es la base del exponente
$X$ es lo que aparece dentro del logaritmo, también puede aparecer entre paréntesis
$b$ es el exponente al que elevamos la base del logaritmo para obtener el número que aparece dentro del logaritmo.

La suma de logaritmos con la misma base se basa en la siguiente regla:

$log_a⁡x+log_a⁡y=log_a⁡(x\cdot y)$

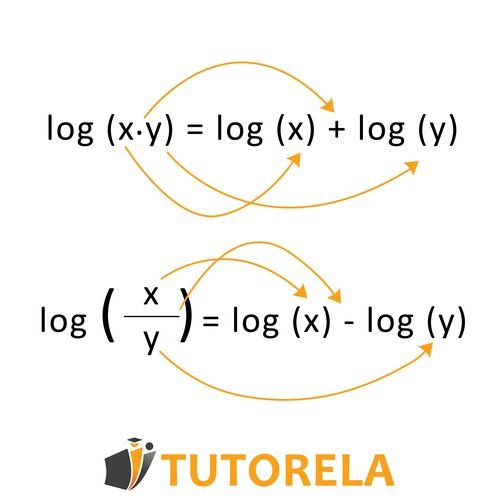
Explicación visual de las reglas logarítmicas que muestra que log(x·y) es igual a log(x) más log(y), y log(x/y) es igual a log(x) menos log(y), con flechas conectando cada parte para mayor claridad.

La suma de logaritmos con diferentes bases se realiza cambiando la base del logaritmo usando la siguiente regla:

$log_aX=\frac{log_{base~que~queremos~cambiar~a}X}{log_{base~que~queremos~cambiar~a}a}$

Fórmula de cambio de base logarítmica ilustrada: logaritmo base b de a es igual a logaritmo base x de a dividido por logaritmo base x de b, con flechas mostrando la transformación desde la forma original.

Explicación completa

Practicar Suma de logaritmos

Pon a prueba tus conocimientos con más de 6 cuestionarios

?=a

$\ln(a+5)+\ln(a+7)=0$

ejemplos con soluciones para Suma de logaritmos

Soluciones paso a paso incluidas

Ejercicio #1

$2\log_82+\log_83=$

Solución Paso a Paso

$2\log_82=\log_82^2=\log_84$

$2\log_82+\log_83=\log_84+\log_83=$

$\log_84\cdot3=\log_812$

Respuesta:

$\log_812$

Solución en video

Ejercicio #2

$3\log_49+8\log_4\frac{1}{3}=$

Solución Paso a Paso

En donde:

$3\log_49=\log_49^3=\log_4729$

$8\log_4\frac{1}{3}=\log_4\left(\frac{1}{3}\right)^8=$

$\log_4\frac{1}{3^8}=\log_4\frac{1}{6561}$

Por lo tanto

$3\log_49+8\log_4\frac{1}{3}=$

$\log_4729+\log_4\frac{1}{6561}$

$\log_ax+\log_ay=\log_axy$

$\left(729\cdot\frac{1}{6561}\right)=\log_4\frac{1}{9}$

$\log_49^{-1}=-\log_49$

Respuesta:

$-\log_49$

Solución en video

Ejercicio #3

$\frac{1}{2}\log_24\times\log_38+\log_39\times\log_37=$

Solución Paso a Paso

Descomponemos en partes

$\log_24=x$

$2^x=4$

$x=2$

$\log_39=x$

$3^x=9$

$x=2$

Reemplazamos en la ecuación

$\frac{1}{2}\cdot2\log_38+2\log_37=$

$1\cdot\log_38+2\log_37=$

$\log_38+\log_37^2=$

$\log_38+\log_349=$

$\log_3\left(8\cdot49\right)=\log_3392$ $x=2$

Respuesta:

$\log_3392$

Solución en video

Ejercicio #4

$\log7x+\log(x+1)-\log7=\log2x-\log x$

$?=x$

Solución Paso a Paso

Domino de definición

$x>0$

$x+1>0$

$x>-1$

$\log7x+\log\left(x+1\right)-\log7=\log2x-\log x$

$\log\frac{7x\cdot\left(x+1\right)}{7}=\log\frac{2x}{x}$

Reducimos por: $7$ y por $X$

$x\left(x+1\right)=2$

$x^2+x-2=0$

$\left(x+2\right)\left(x-1\right)=0$

$x+2=0$

$x=-2$

No dominio de definición $x>0$

$x-1=0$

$x=1$

Dominio de definición

Respuesta:

$1$

Solución en video

Ejercicio #5

$\log_{10}3+\log_{10}4=$

Solución Paso a Paso

Respuesta:

$\log_{10}12$

Solución en video

Preguntas Frecuentes

Todo lo que necesitas saber Suma de logaritmos

¿Cómo se suman logaritmos con la misma base?

Para sumar logaritmos con la misma base, usa la regla: log_a(x) + log_a(y) = log_a(x·y). Simplemente multiplica los números dentro de los logaritmos y mantén la misma base. Por ejemplo: log_8(32) + log_8(2) = log_8(32·2) = log_8(64) = 2.

¿Se pueden sumar logaritmos con diferentes bases directamente?

No, no se pueden sumar logaritmos con diferentes bases directamente. Primero debes convertir ambos logaritmos a la misma base usando la fórmula de cambio de base: log_a(x) = log_b(x)/log_b(a). Luego podrás aplicar las reglas de suma.

¿Cuál es la fórmula para cambiar la base de un logaritmo?

La fórmula de cambio de base es: log_a(x) = log_b(x)/log_b(a). En el numerador escribes el logaritmo con la nueva base y el mismo argumento, en el denominador escribes el logaritmo con la nueva base y la base original como argumento.

¿Qué significa log_a(x) + log_a(y) = log_a(x·y)?

Esta propiedad establece que la suma de logaritmos con la misma base equivale al logaritmo del producto de sus argumentos. Es una de las propiedades fundamentales de los logaritmos que simplifica muchos cálculos matemáticos.

¿Cómo resolver log_8(32) + log_8(2)?

Sigue estos pasos: 1) Aplica la regla de suma: log_8(32) + log_8(2) = log_8(32·2), 2) Calcula el producto: log_8(64), 3) Determina a qué potencia elevar 8 para obtener 64: 8² = 64, 4) La respuesta es 2.

¿Cuándo usar el cambio de base en logaritmos?

Usa el cambio de base cuando necesites sumar, restar o comparar logaritmos con bases diferentes. También es útil cuando quieres convertir a una base más simple (como base 10 o base e) para facilitar los cálculos.

¿Qué errores comunes se cometen al sumar logaritmos?

Los errores más comunes incluyen: 1) Intentar sumar logaritmos con bases diferentes sin convertir, 2) Confundir suma con multiplicación (log_a(x) + log_a(y) ≠ log_a(x+y)), 3) Olvidar que la suma de logaritmos equivale al logaritmo del producto, no de la suma.

¿Cómo verificar la respuesta de una suma de logaritmos?

Para verificar: 1) Sustituye tu respuesta en la ecuación original, 2) Calcula cada logaritmo por separado usando la definición, 3) Comprueba que ambos lados de la ecuación sean iguales. También puedes usar una calculadora para verificar valores decimales.

Continúa tu viaje matemático

Domina primero la Suma de logaritmos, luego avanza a estos temas relacionados que construyen sobre tus habilidades con fracciones

Temas que se aprenden en secciones posteriores

Practica por Tipo de Pregunta

Elige tu estilo de aprendizaje y formato de práctica preferido para problemas de fracciones

Aplicación de la fórmula Desigualdad El resultado en una ecuación cuadrática Uso de múltiples reglas Uso de variables