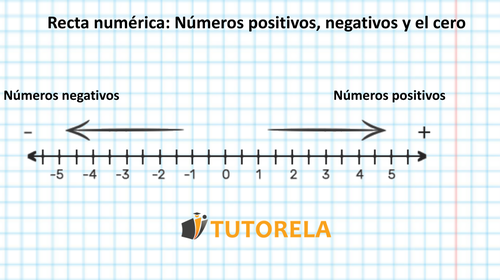
Los números positivos, negativos y el cero son un tema fundamental en álgebra, es muy fácil de entenderlo trazando una recta numérica en la cual el cero se ubica en medio.
- El cero es nuestro punto de referencia.
- Los números positivos son los mismos números que usamos hasta el día de hoy y están ubicados a la derecha del cero. Ahora que estamos comenzando a estudiar el tema de los números positivos y negativos, veremos un signo antes de los positivos, el signo más (+), para dejar claro que se trata de un número positivo, pero, más adelante, luego de que entendamos bien el tema, lo suprimiremos.
- Los números negativos son los que están ubicados del lado izquierdo del cero y tienen un signo menos (-). A diferencia de lo que ocurre con los números positivos, el signo menos aparecerá siempre junto a los números negativos para indicar que realmente se trata de números negativos.
Lo ilustraremos en la recta numérica: