Preguntas Frecuentes
Todo lo que necesitas saber Solución algebraica
¿Cuándo es mejor usar el método de sustitución en sistemas de ecuaciones?
+ El método de sustitución es ideal cuando una incógnita tiene coeficiente 1 o -1, o cuando puedes aislar fácilmente una variable sin crear fracciones. Por ejemplo, en la ecuación 3y - x = 4, es conveniente despejar x porque tiene coeficiente -1.
¿Cómo sé si debo usar el método de igualación?
+ Usa el método de igualación cuando los coeficientes de una misma incógnita son iguales, opuestos, o múltiplos simples entre sí. Si tienes 5x + 6y = 7 y 5x + 4y = 13, puedes restar directamente las ecuaciones para eliminar la x.
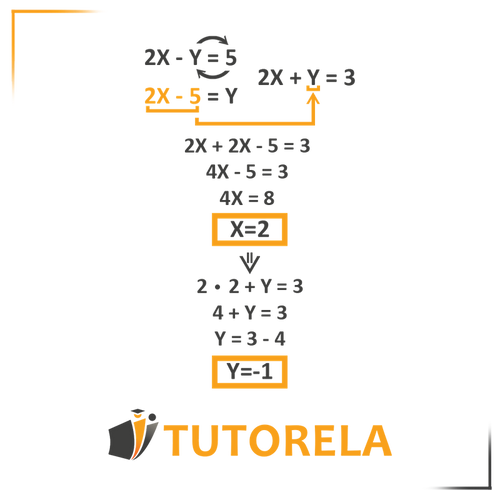
¿Qué pasos sigo para resolver por el método de sustitución?
+ Los pasos son: 1) Aislar una incógnita en cualquier ecuación, 2) Sustituir esa expresión en la otra ecuación, 3) Resolver la ecuación resultante con una sola incógnita, 4) Sustituir el valor encontrado para hallar la otra incógnita.
¿Cómo igualo coeficientes cuando no son iguales ni opuestos?
+ Multiplica una o ambas ecuaciones por constantes apropiadas para hacer que los coeficientes de una incógnita sean iguales u opuestos. Por ejemplo, si tienes coeficientes 3 y 6 para x, multiplica la primera ecuación por 2 para obtener coeficientes iguales.
¿Qué significa cuando obtengo 0 = 5 al resolver un sistema?
+ Cuando obtienes una expresión falsa como 0 = 5, significa que el sistema no tiene solución. Esto ocurre cuando las ecuaciones representan rectas paralelas que nunca se intersectan.
¿Cómo resuelvo problemas verbales con sistemas de ecuaciones?
+ Primero identifica las dos incógnitas y asígnalas a variables (x, y). Luego traduce cada condición del problema a una ecuación matemática. Finalmente, resuelve el sistema usando sustitución o igualación y verifica que la respuesta tenga sentido en el contexto.
¿Qué hago si obtengo 0 = 0 al resolver un sistema?
+ Cuando obtienes 0 = 0, el sistema tiene infinitas soluciones. Esto significa que las dos ecuaciones son equivalentes y representan la misma recta, por lo que cualquier punto de esa recta es solución del sistema.
¿Cómo verifico si mi solución es correcta?
+ Sustituye los valores encontrados (x, y) en ambas ecuaciones originales. Si ambas ecuaciones se cumplen (los lados izquierdo y derecho son iguales), entonces tu solución es correcta. Esta verificación es esencial para confirmar tu trabajo.