?=a $$ \ln(a+5)+\ln(a+7)=0 $$

$$ -6-\sqrt{2}\text{ \& }-6+\sqrt{2} $$

Suma de Logaritmos

La definición de un logaritmo es:

$log_a⁡x=b$
$X=a^b$

Donde:
$a$ es la base del exponente
$X$ es lo que aparece dentro del logaritmo, también puede aparecer entre paréntesis
$b$ es el exponente al que elevamos la base del logaritmo para obtener el número que aparece dentro del logaritmo.

La suma de logaritmos con la misma base se basa en la siguiente regla:

$log_a⁡x+log_a⁡y=log_a⁡(x\cdot y)$

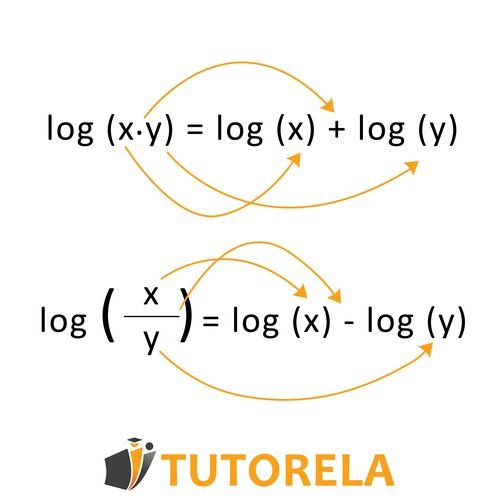
Explicación visual de las reglas logarítmicas que muestra que log(x·y) es igual a log(x) más log(y), y log(x/y) es igual a log(x) menos log(y), con flechas conectando cada parte para mayor claridad.

La suma de logaritmos con diferentes bases se realiza cambiando la base del logaritmo usando la siguiente regla:

$log_aX=\frac{log_{base~que~queremos~cambiar~a}X}{log_{base~que~queremos~cambiar~a}a}$

Fórmula de cambio de base logarítmica ilustrada: logaritmo base b de a es igual a logaritmo base x de a dividido por logaritmo base x de b, con flechas mostrando la transformación desde la forma original.

Explicación completa

Ir a prácticas

¡Pruébate en suma de logaritmos!

$\log_{10}3+\log_{10}4=$

Quiz y otros ejercicios

Suma de Logaritmos

Recordatorio - Logaritmos Definición: log_b(x) = y significa que b^y = x Propiedades: 1. log_b(1) = 0 2. log_b(b) = 1 3. log_b(b^n) = n Reglas: 1. log_b(x·y) = log_b(x) + log_b(y) 2. log_b(x/y) = log_b(x) - log_b(y) 3. log_b(x^n) = n·log_b(x) Cambio de base: log_b(x) = log_a(x)/log_a(b)

Primero, recordemos cuál es la definición de $log$ ?
$log_a⁡x=b$
Donde $a$ es la base del logaritmo (usualmente $10$ )
$b$ es el exponente al cual elevamos $a$
$X$ que a veces aparece entre paréntesis, es el número que obtenemos cuando $a$ se eleva a la potencia de $b$ , también llamado el número dentro del logaritmo.
En otras palabras:
$X=a^b$

Por ejemplo, si nos encontramos con un ejercicio como este:
$log_6⁡36=$

Determina a qué potencia debemos elevar $6$ para obtener $36$ ....?
La respuesta es la potencia de $2$ y por lo tanto la solución es $2$ .

Suma de logaritmos con la misma base

Para sumar fácilmente logaritmos con la misma base, solo necesitas conocer la siguiente regla:
$log_a⁡x+log_a⁡y=log_a⁡(x\cdot y)$
La regla establece que si quieres sumar $2$ logaritmos con la misma base, puedes escribirlos como $1$ logaritmo y multiplicar los números dentro del logaritmo. Esto frecuentemente simplificará el proceso de solución.

Veamos un ejemplo:
$log_8⁡32+log_8⁡2=$
Si no supieras lo anterior, casi seguramente te encontrarías con un problema.
¿A qué potencia debemos elevar $8$ para obtener $2$ ?... ¿Y a qué potencia debemos elevar $8$ para obtener $32$ ?
¡Aquí es donde la regla que aprendiste anteriormente es útil!
Todo lo que necesitas hacer es multiplicar los números que aparecen en el logaritmo manteniendo la misma base– $8$ .
Así obtenemos lo siguiente:
$log_8⁡32+log_8⁡2=log_8⁡(32\cdot2)$
Y también:
$log_8⁡(32\cdot2)=log_8⁡(64)$
¡Ahora es mucho más fácil resolver la ecuación!
Sabemos que necesitamos elevar $8$ a la potencia de $2$ para obtener $64$ y por lo tanto la respuesta completa a este ejercicio es $2$ .
$log_8⁡(64)=2$

Nota - Esta regla es válida solo en casos donde la base es idéntica. Si la base no fuera la misma en ambos logaritmos, no podríamos usar esta regla.
¡Recuerda!
Cuando tienes la misma base en ambos logaritmos y una operación de suma entre ellos, puedes multiplicar los números dentro de los logaritmos y mantener la base como está - suma~multiplicación

¡Únete a 30,000 estudiantes destacados en matemáticas!

Práctica ilimitada, guía de expertos: mejora tus habilidades matemáticas hoy

Comprueba tu conocimiento

Ejercicio 1

$\log_24+\log_25=$

Ejercicio 2

$\log_974+\log_9\frac{1}{2}=$

Ejercicio 3

$2\log_82+\log_83=$

Suma de Logaritmos con Diferentes Bases

¿Qué sucede cuando hay un ejercicio de suma con logaritmos de diferentes bases?
Para sumar logaritmos con diferentes bases, es importante conocer la regla que nos permite cambiar la base de un logaritmo.
El objetivo es convertir ambos logaritmos a la misma base.

¿Cómo se cambia la base de un logaritmo?

Conoce la regla del cambio de base de logaritmos:
$log_aX=\frac{log_{la~base~a~la~que~queremos~cambiar}X}{log_{la~base~a~la~que~queremos~cambiar}a}$

Ahora para la explicación:
Cuando tenemos un logaritmo con base $a$ por ejemplo y queremos convertirlo a otro logaritmo:

Dibuja una línea de fracción.
En el numerador, escribe el logaritmo con la nueva base deseada y lo que estaba en el logaritmo original.
En el denominador, escribe el logaritmo con la nueva base deseada y dentro pon la base del logaritmo original.

Veamos un ejemplo:

$log_8⁡16=$
Convierte el siguiente logaritmo a base $2$ :

$log_8⁡16=\frac{log_26}{log_28}$

En el numerador, escribiremos logaritmo base $2$ , que es la base a la que queremos convertir. El número dentro del logaritmo en el numerador será el número original que aparece dentro del logaritmo, que es $16$ .

En el denominador, escribiremos nuevamente logaritmo base $2$ , la base a la que queremos convertir, pero esta vez, el número dentro del logaritmo será la base original - que es $8$
Ahora podemos resolver el problema fácilmente. Obtenemos lo siguiente:

$\frac{log_2⁡16}{log_2⁡8} =\frac{4}{3}$

Recuerda - siempre que quieras convertir a una base logarítmica diferente, necesitarás convertir el logaritmo a una fracción según la regla que acabas de aprender.
Ejercicio avanzado: Ahora puedes resolver sumas de logaritmos con diferentes bases:
$log_{25}⁡x+ log_5⁡x=3$
Queremos convertir ambos logaritmos a la misma base y usualmente elegiremos la base menor - $5$ .
Por lo tanto:

$log_{25⁡}x=\frac{log_5⁡x}{log_5⁡25}$
Ahora reescribamos el ejercicio e insertemos nuestros datos:

$\frac{log_5⁡x}{log_5⁡25} ⁡+ log_5⁡x=3$

Insertemos $log_5⁡25=2$
y obtengamos lo siguiente:
$\frac{log_5⁡x}{2}⁡+ log_5⁡x=3$
$0.5⁡log_5⁡x+log_5⁡x=3$

$1.5 log_5⁡x=3$
$log_5⁡x=2$
$x=5^2$

Obtuvimos la solución:
$x=25$

¿Sabes cuál es la respuesta?

Ejercicio 1

$3\log_49+8\log_4\frac{1}{3}=$

Ejercicio 2

$\frac{1}{2}\log_24\times\log_38+\log_39\times\log_37=$

Ejercicio 3

$\log_2x+\log_2\frac{x}{2}=5$

?=x

ejemplos con soluciones para Suma de logaritmos

Ejercicio #1

$2\log_82+\log_83=$

Solución en video

Solución Paso a Paso

$2\log_82=\log_82^2=\log_84$

$2\log_82+\log_83=\log_84+\log_83=$

$\log_84\cdot3=\log_812$

Respuesta

$\log_812$

Ejercicio #2

$3\log_49+8\log_4\frac{1}{3}=$

Solución en video

Solución Paso a Paso

En donde:

$3\log_49=\log_49^3=\log_4729$

$8\log_4\frac{1}{3}=\log_4\left(\frac{1}{3}\right)^8=$

$\log_4\frac{1}{3^8}=\log_4\frac{1}{6561}$

Por lo tanto

$3\log_49+8\log_4\frac{1}{3}=$

$\log_4729+\log_4\frac{1}{6561}$

$\log_ax+\log_ay=\log_axy$

$\left(729\cdot\frac{1}{6561}\right)=\log_4\frac{1}{9}$

$\log_49^{-1}=-\log_49$

Respuesta

$-\log_49$

Ejercicio #3

$\frac{1}{2}\log_24\times\log_38+\log_39\times\log_37=$

Solución en video

Solución Paso a Paso

Descomponemos en partes

$\log_24=x$

$2^x=4$

$x=2$

$\log_39=x$

$3^x=9$

$x=2$

Reemplazamos en la ecuación

$\frac{1}{2}\cdot2\log_38+2\log_37=$

$1\cdot\log_38+2\log_37=$

$\log_38+\log_37^2=$

$\log_38+\log_349=$

$\log_3\left(8\cdot49\right)=\log_3392$ $x=2$

Respuesta

$\log_3392$

Ejercicio #4

$\log7x+\log(x+1)-\log7=\log2x-\log x$

$?=x$

Solución en video

Solución Paso a Paso

Domino de definición

$x>0$

$x+1>0$

$x>-1$

$\log7x+\log\left(x+1\right)-\log7=\log2x-\log x$

$\log\frac{7x\cdot\left(x+1\right)}{7}=\log\frac{2x}{x}$

Reducimos por: $7$ y por $X$

$x\left(x+1\right)=2$

$x^2+x-2=0$

$\left(x+2\right)\left(x-1\right)=0$

$x+2=0$

$x=-2$

No dominio de definición $x>0$

$x-1=0$

$x=1$

Dominio de definición

Respuesta

$1$

Ejercicio #5

$\log_{10}3+\log_{10}4=$

Solución en video

Respuesta

$\log_{10}12$

Ir a prácticas